Chapter 3 Statistical Distributions

Much of this chapter is based strongly (for large parts identical) on the STAT444 course by Derek Sonderegger.

Fundamental to the study of statistics is the idea of statistical distributions. For example, we will often assume that some population we are interested in has a particular distribution such as the Normal distrubution. In the past, we would have used statistical tables, but fortunately with R these are mostly not used.

3.1 Visualising distributions

The mosaic package provides a very useful routine for visualizing a distribution.

For example, to see the normal distribution with mean \(\mu=10\) and standard deviation \(\sigma=2\), we use

mosaic::plotDist('norm', mean=10, sd=2)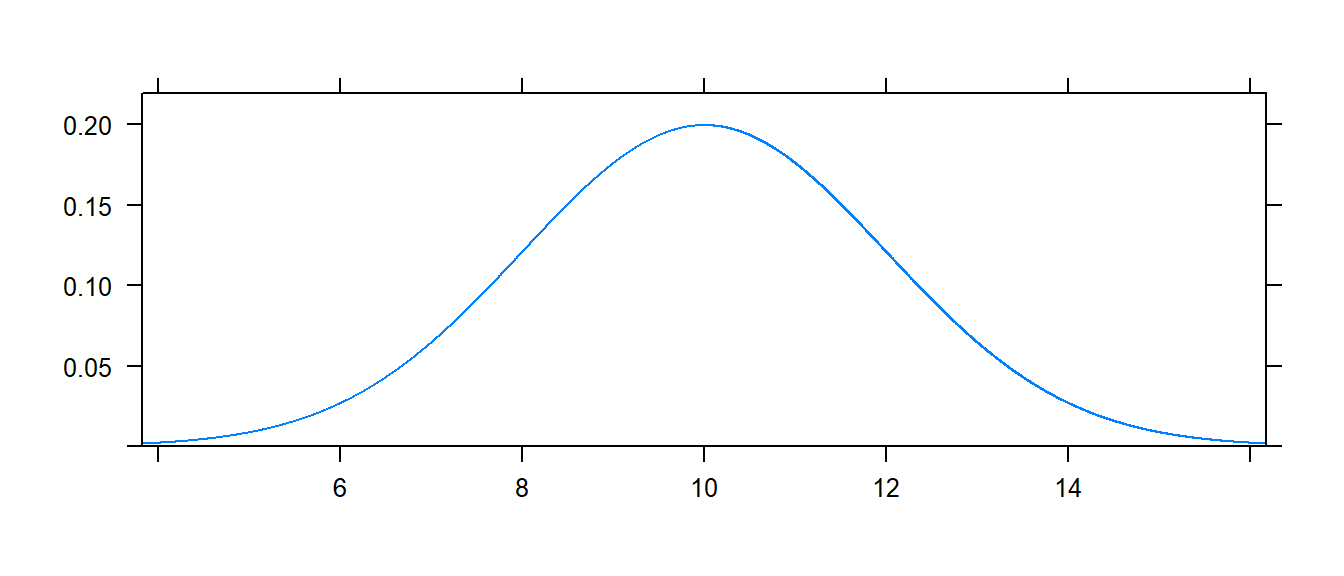

This function works for discrete distributions such as the binomial distribution as well.

mosaic::plotDist('binom', size=10, prob=.3)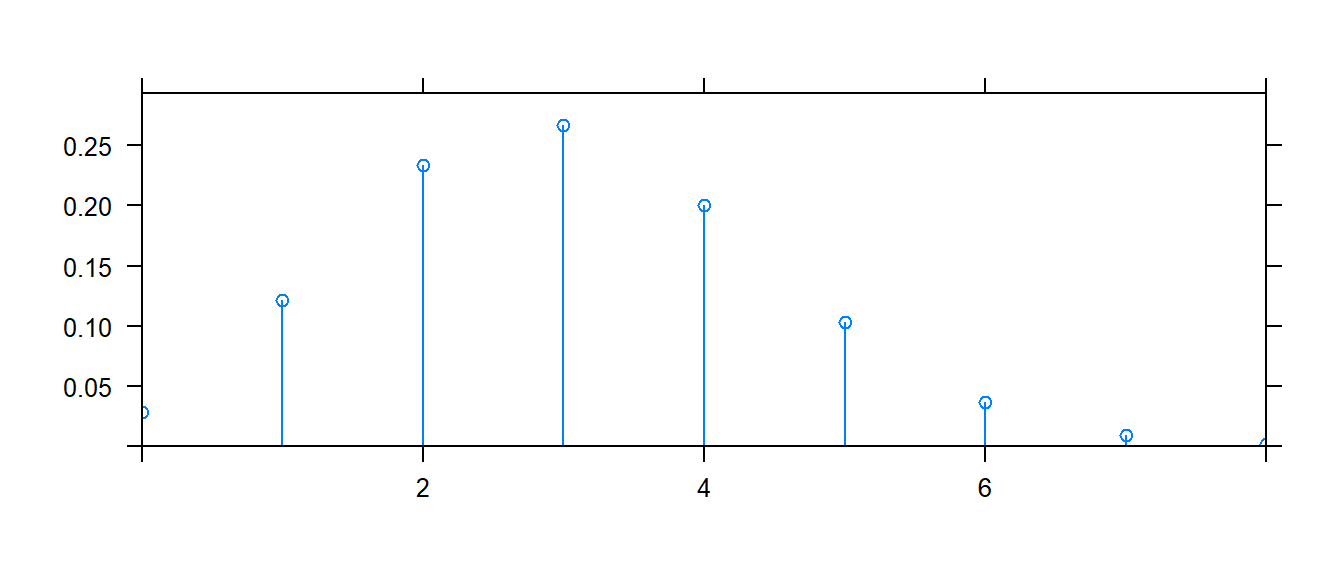

Try changing the parameters of the distribution- does it do what you expect?

Note above we are using a function in the mosaic package by specifying it via PackageName::FunctionName() format.

3.2 Statistical distributions in R

In general we need to do two things in R: we need to tell R what we want to do with the distribution, and which distribution we have.

For example, if we want a random draw from a normal distribution, we use the rnorm function. If we want the pdf of the Poisson distribution, we use the dpois distribution.

First part : what do we want to do Second Part : which distribution
d, p, q, or r e.g. norm, pois, t, binom, unif

We explain this more in the next sections.

3.3 Example Distributions

R has many built-in distributions (with many more available in various packages). For reference below is a list of common distributions you might find in an introductory statistics course, their R name and a list of necessary parameters.

Distribution R Stem Parameters Parameter Interpretation
Binomial binom size
prob		 Number of Trials Probability of Success (per Trial)
Exponential exp rate Inverse of mean of the distribution
Normal norm mean=0
sd=1		 Mean of the distribution
Standard deviation
Uniform (continuous) unif min=0
max=1		 Minimum of the distribution
Maximum of the distribution
t t df Degrees of freedom
F f df1
df2		 Numerator Degrees of freedom Denominator Degrees of freedom

Most of these parameters have some default value if it is not specified.

3.4 Base R functions

All the probability distributions available in R are accessed in exactly the same way, using a d-function, p-function, q-function, and r-function. For the rest of this section we assume that \(X\) is a random variable from the distribution of interest and \(x\) is some possible value that \(X\) could take.

Function Result
d-function(x) T This PDF for a continuous random variable, or the PMF for a discrete random variable. The distance from the x-axis to the curve at a given \(x\).
p-function(x) The CDF: the probability of an outcome less than or equal to `x.
q-function(q) The q quantile of the distribution (opposite of p-function). What proportion of the distribution lies below (or above) q
r-function(n) Generate \(n\) random observations from the distribution

For each distribution in R, there will be this set of functions but we replace the “-function” with the distribution name or a shortened version, such as dnorm or pbinom. As in the table above, norm, exp, binom, t, f are the names for the normal, exponential, binomial, T and F distributions.

d-function

The d-function calculates the distance from the x-axis to the probability density curve or height of a probability mass function. The “d” actually stands for density. Notice that for discrete distributions, this is the probability of observing that particular value, while for continuous distributions, the height doesn’t have a nice physical interpretation.

We start with an example of the Binomial distribution. For \(X\sim Binomial\left(n=10,\pi=.2\right)\), suppose we wanted to know \(P(X=0)\). We know the probability mass function is \[P\left(X=x\right)={n \choose x}\pi^{x}\left(1-\pi\right)^{n-x}\] thus \[P\left(X=0\right) = {10 \choose 0}\,0.2^{0}\left(0.8\right)^{10} = 1\cdot1\cdot0.8^{10} \approx 0.107\] but that calculation is fairly tedious. To get R to do the same calculation, we just need the height of the probability mass function at \(0\). To do this calculation, we need to know the x value we are interested in along with the distribution parameters for the binomial distribution \(n\) and \(\pi\).

The first thing we should do is check the help file for the binomial distribution functions to see what parameters are needed and what they are named.

?dbinom

The help file shows us the parameters \(n\) and \(\pi\) are called size and prob respectively. So to calculate the probability that \(X=0\) we would use the following command:

dbinom(0, size=10, prob=.2)
## [1] 0.1073742

p-function

Often we are interested in the probability of observing some value or anything less (In probability theory, we call this the cumulative density function or CDF).

Let’s again look at the same binomial distribution, where \(X\sim Binomial\left(n=10,\pi=0.2\right)\). Suppose I want to know the probability of observing a 0, 1, or 2. That is, what is \(P\left(X\le2\right)\)? I could use the \(d\)-function to find the probability of each and add them up.

dbinom(0, size=10, prob=.2)   +       #   P(X==0) +
  dbinom(1, size=10, prob=.2) +       #     P(X==1) +
  dbinom(2, size=10, prob=.2)         #     P(X==2)
## [1] 0.6777995

but this would get tedious for binomial distributions with a large number of trials. The shortcut is to use the pbinom() function.

pbinom(2, size=10, prob=.2)
## [1] 0.6777995

For discrete distributions, you must be careful because R will give you the probability of less than or equal to 2. If you wanted less than two, you should use dbinom(1,10,.2).

The normal distribution works similarly. Suppose for \(Z\sim N\left(0,1\right)\) and we wanted to know \(P\left(Z\le-1\right)\)?

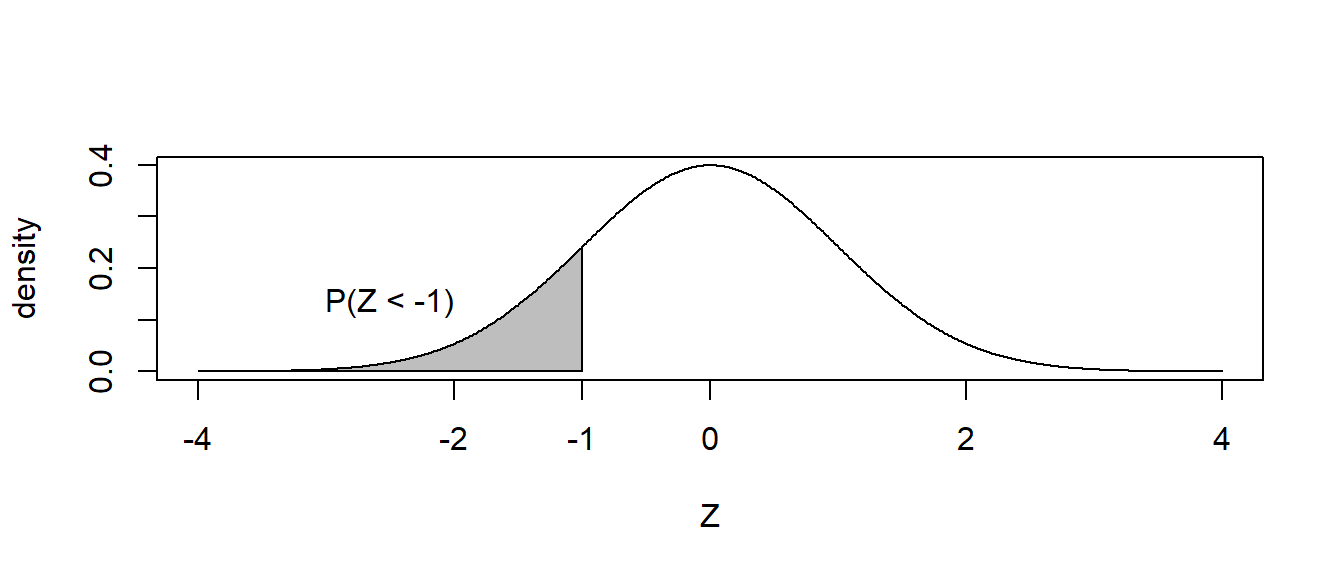
The answer is easily found via pnorm().

pnorm(-1)
## [1] 0.1586553

Notice for continuous random variables, the probability \(P\left(Z=-1\right)=0\) so we can ignore the issue of “less than” vs “less than or equal to”.

Often we will want to know the probability of a random variable being greater than some value. That is, we might want to find \(P\left(Z \ge -1\right)\). There are a number of tricks we could use. Notably \[P\left(Z\ge-1\right) = P\left(Z\le1\right)=1-P\left(Z<-1\right)\] but sometimes I’m lazy and would like to tell R to give me the area to the right instead of area to the left (which is the default). This can be done by setting the argument lower.tail=FALSE.

The mosaic package includes an augmented version of the pnorm() function called xpnorm() that calculates the same number but includes some extra information and produces a pretty graph to help us understand what we just calculated and do the tedious “1 minus” calculation to find the upper area. Fortunately this x-variant exists for the Normal, Chi-squared, F, Gamma continuous distributions and the discrete Poisson, Geometric, and Binomial distributions.

mosaic::xpnorm(-1)
## 
## If X ~ N(0, 1), then
##  P(X <= -1) = P(Z <= -1) = 0.1587
##  P(X >  -1) = P(Z >  -1) = 0.8413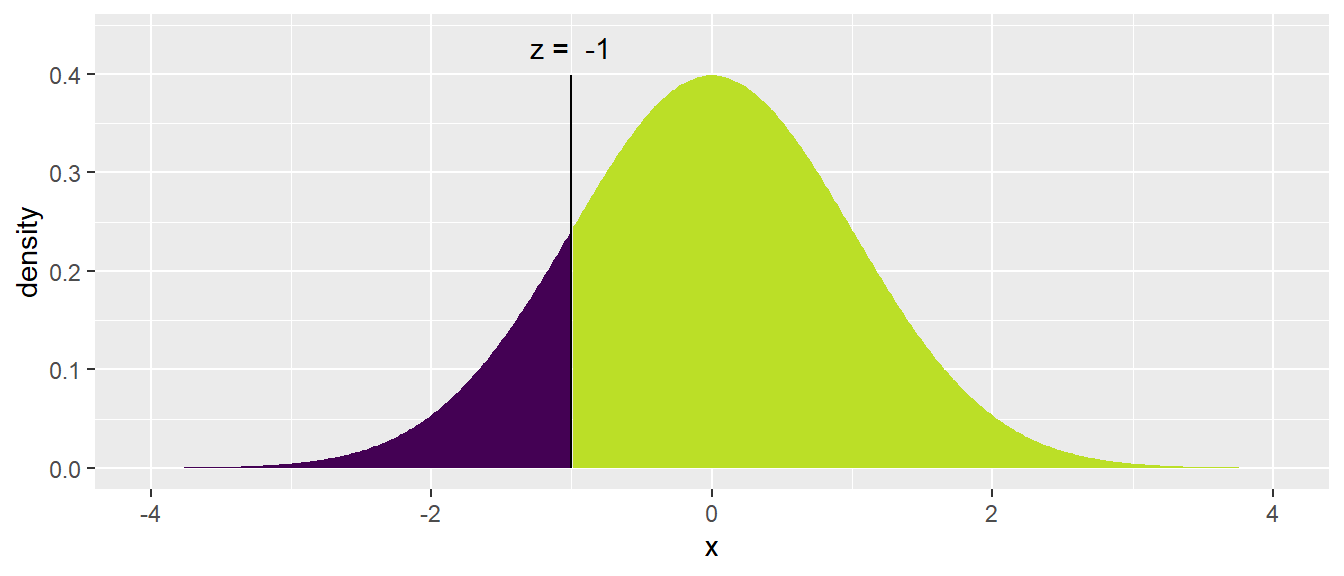
## 

## [1] 0.1586553

q-function

We will also sometimes find ourselves asking for the quantiles of a distribution. For example, we might want to find the 30th percentile, or the 0.30 quantile, which is the value such that 30% of the distribution is less than it, and 70% is greater. Mathematically, we wish to find the value \(z\) such that \(P(Z<z)=0.30\).

R gives us a handy way to do this with the qnorm() function and the mosaic package provides a nice visualization using the augmented xqnorm().

mosaic::xqnorm(0.30)   # Give me the value along with a pretty picture
## 
## If X ~ N(0, 1), then
##  P(X <= -0.5244005) = 0.3
##  P(X >  -0.5244005) = 0.7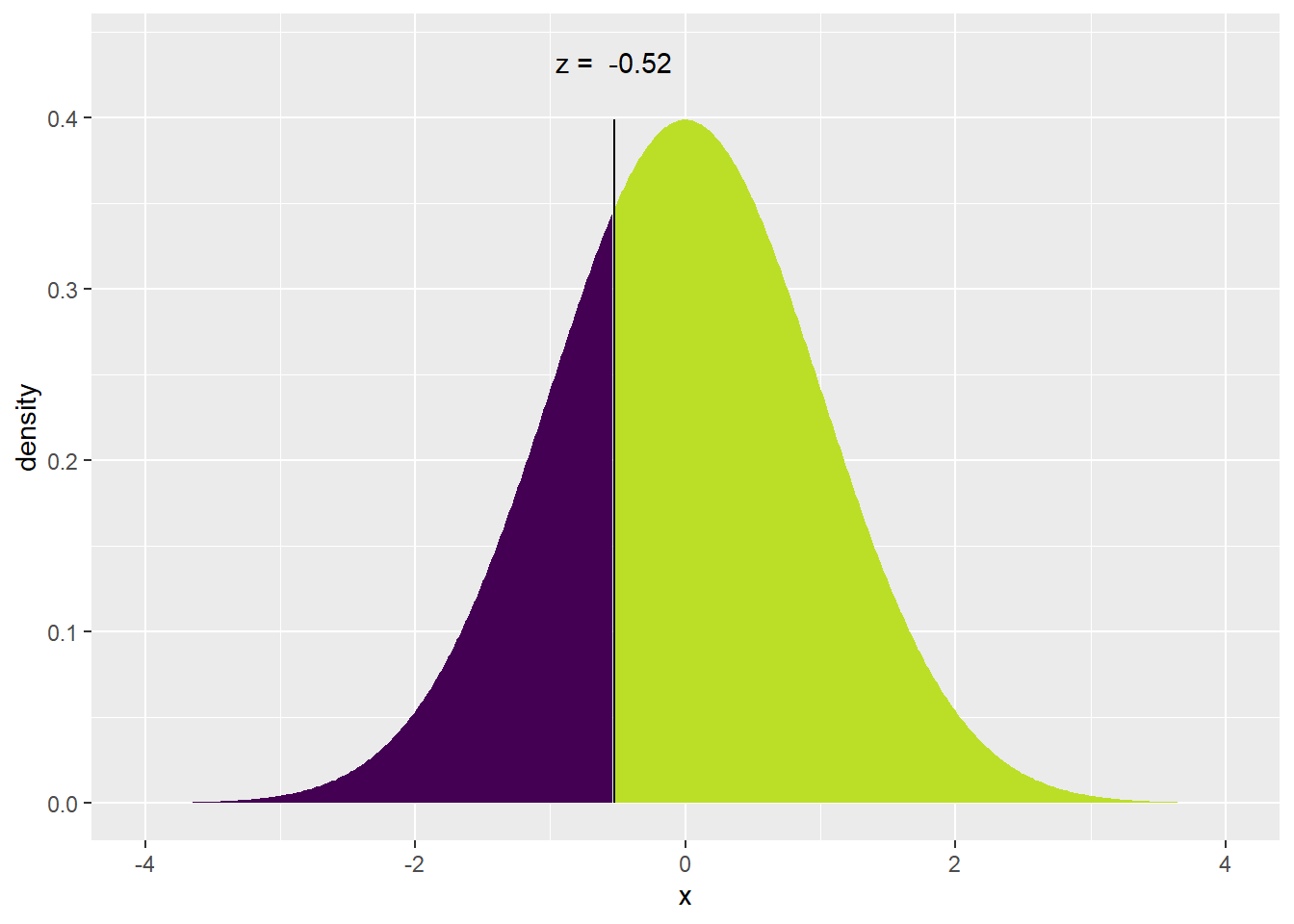
## 

## [1] -0.5244005
qnorm(.30)             # No pretty picture, just the value
## [1] -0.5244005

Notice that the p-function is the inverse of the q-function.

r-function

Finally, to generate random data from a particular distribution, we use the r-function. The first argument to this function the number of random variables to draw and any remaining arguments are the parameters of the distribution.

rnorm(5, mean=20, sd=2)   
## [1] 22.76534 19.69489 21.83924 20.06909 21.00385
rbinom(4, size=10, prob=.8)
## [1]  9  7  7 10

3.5 Exercises

  1. We will examine how to use the probability mass function (a.k.a. d-function) and cumulative probability function (a.k.a. p-function) for the Poisson distribution.
    1. Create a graph of the distribution of a Poisson random variable with rate parameter \(\lambda=2\) using the mosaic function plotDist().
    2. Calculate the probability that a Poisson random variable (with rate parameter \(\lambda=2\) ) is exactly equal to 3 using the dpois() function. Be sure that this value matches the graphed distribution in part (a).
    3. For a Poisson random variable with rate parameter \(\lambda=2\), calculate the probability it is less than or equal to 3, by summing the four values returned by the Poisson d-function.
    4. Perform the same calculation as the previous question but using the cumulative probability function ppois().
  2. We will examine how to use the cumulative probability functions (a.k.a. p-functions) for the normal and exponential distributions.
    1. Use the mosaic function plotDist() to produce a graph of the standard normal distribution (that is a normal distribution with mean \(\mu=0\) and standard deviation \(\sigma=1\).
    2. For a standard normal, use the pnorm() function or its mosaic augmented version xpnorm() to calculate
      1. \(P\left(Z<-1\right)\)
      2. \(P\left(Z\ge1.5\right)\)
    3. Use the mosaic function plotDist() to produce a graph of an exponential distribution with rate parameter 2.
    4. Suppose that \(Y\sim Exp\left(2\right)\), as above, use the pexp() function to calculate \(P\left(Y \le 1 \right)\). (Unfortunately there isn’t a mosaic augmented xpexp() function.)
  3. We next examine how to calculate quantile values for the normal and exponential distributions using R’s q-functions.
    1. Find the value of a standard normal distribution (\(\mu=0\), \(\sigma=1\)) such that 5% of the distribution is to the left of the value using the qnorm() function or the mosaic augmented version xqnorm().
    2. Find the value of an exponential distribution with rate 2 such that 60% of the distribution is less than it using the qexp() function.
  4. Finally we will look at generating random deviates from a distribution.
    1. Generate a single value from a uniform distribution with minimum 0, and maximum 1 using the runif() function. Repeat this step several times and confirm you are getting different values each time.
    2. Generate a sample of size 20 from the same uniform distribution and save it as the vector x using the following:
        x <- runif(20, min=0, max=1)

Then produce a histogram of the sample using the function hist(x).

  1. Generate a sample of 2000 from a normal distribution with mean=10 and standard deviation sd=2 using the rnorm() function. Create a histogram the the resulting sample.