Chapter 5 Flow Control in R

In this course, the emphasis is on using R to do statistics, rather than as a programming language. However, like every computing language, R allows us to change the order in which we run code, and evaluate code conditionally on some properties being true, and we need to know the basics of how to do this.

5.1 True or false

A data type we need to know about in R is the logical data type, which takes the value TRUE or FALSE.

At it’s simplest form, we can use this to do a number of tests:

1<2 
## [1] TRUE
3>5
## [1] FALSE
4==4
## [1] TRUE
4==5
## [1] FALSE
1<=2
## [1] TRUE
2>=2
## [1] TRUE
3<=2
## [1] FALSE

Note that in R, == is used for testing equality, and = can be used for assignment, which is one of the reasons I prefer assigning variables using x<-2 rather than x=2.

Of course, we can test variables against a logical condition, and indeed many variables can be tested at once.

x<-3 #Assignment
x<2
## [1] FALSE
y<-c(1,2,3,4,5,6)
y<2
## [1]  TRUE FALSE FALSE FALSE FALSE FALSE
y<x
## [1]  TRUE  TRUE FALSE FALSE FALSE FALSE

5.1.1 Logical tests

The command ifelse() works quite well and it responds correctly to vectors. The syntax is ifelse( logical.expression, TrueValue, FalseValue ).

x<-3
ifelse( x>4, y<-7, y<-"Birmingham" )
## [1] "Birmingham"
str(y)
##  chr "Birmingham"
x<-5
ifelse( x>4, y<-7, y<-"Birmingham" )
## [1] 7
str(y)
##  num 7

5.1.2 General if else

While programming, I often need to perform expressions that are more complicated than what the ifelse() command can do. The general format of an if or an if else is presented here.

# Simplest version
if( logical.test ){
  expression        # can be many lines of code
}

# Including the optional else
if( logical.test ){
  expression
}else{
  expression
}

where the else part is optional. The test expression inside the if() is evaluated and if it is true, then the subsequent statement is executed. If the test expression is false, the next statement is skipped. If we want multiple statements to be executed (or skipped), we will wrap those expressions in curly brackets { }.

Suppose that I have a piece of code that generates a Bernoulli random variable (1 with probability \(p\) and 0 with probability \(1-p\)). This is one way to do it in R:

rbinom(n=1, size=1, prob=0.5)
## [1] 0

I’d now like to label it head or tails instead of one or zero.

# Flip the coin, and we get a 0 or 1
result <- rbinom(n=1, size=1, prob=0.5)
result
## [1] 1
# convert the 0/1 to Tail/Head
if( result == 0 ){
  result <- 'Tail'
  print(" in the if statement, got a Tail! ")
}else{
  result <- 'Head'
  print("In the else part!") 
}
## [1] "In the else part!"
result
## [1] "Head"

Run this code several times until you get both cases several times. Notice that in the Environment tab in RStudio, the value of the variable result changes as you execute the code repeatedly.

5.2 For Loops

Throughout most of the rest of the course, we’re going to use R to do something many times. Like many computer languages, one of the simplest ways to do this is the ‘for’ loop.

Let’s suppose we want to find the first 10 terms of the Fibonacci sequence. \[x_1 = 1, x_2 = 1, x_i = x_{i−1} + x_{i−2},\] where each term is the sum of the two previous terms.

We can use a for loop to find the first 10 terms in the sequence

x <- c() # at first x is an empty vector
x[1] <- 1
x[2] <- 1
for (i in 3:10) {
x[i] <- x[i-1] + x[i-2]
}
head(x,5) # gives the first 5 Fibbonaci numbers
## [1] 1 1 2 3 5
x[10] # gives the 10th Fibbonaci number
## [1] 55
x[10]/x[9] # gives the ratio of the 10th and the 9th Fibbonaci Numbers
## [1] 1.617647

Try changing the value in the loop- can you calculate the 100th Fibbonaci number?

5.2.1 More on for loops

You can loop through elements of any vector (instead of 1:10). For example

famous_statisticians <- c("Gauss", "Gosset", "Blackwell")
for(item in famous_statisticians) {
print(item)
}
## [1] "Gauss"
## [1] "Gosset"
## [1] "Blackwell"

5.3 Nested loops

We can also use nested loops- where we loop over two variables.

The following code creates a 5 × 5 matrix with (i, j)-th element equal to i + j

X <- matrix(NA, 5, 5)
for(i in 1:5) {
for(j in 1:5) {
X[i, j] <- i + j
}
}
X
##      [,1] [,2] [,3] [,4] [,5]
## [1,]    2    3    4    5    6
## [2,]    3    4    5    6    7
## [3,]    4    5    6    7    8
## [4,]    5    6    7    8    9
## [5,]    6    7    8    9   10

Note that we haven’t previously encountered matrices, but this is how they work in R. Essentially, R just sees them as a special type of data frame.

We can then add matrices together in the normal way, or multiply them together.

X+X # Usual matrix addition
##      [,1] [,2] [,3] [,4] [,5]
## [1,]    4    6    8   10   12
## [2,]    6    8   10   12   14
## [3,]    8   10   12   14   16
## [4,]   10   12   14   16   18
## [5,]   12   14   16   18   20
X%*%X # Usual matrix multiplication. Note the format.
##      [,1] [,2] [,3] [,4] [,5]
## [1,]   90  110  130  150  170
## [2,]  110  135  160  185  210
## [3,]  130  160  190  220  250
## [4,]  150  185  220  255  290
## [5,]  170  210  250  290  330
X*X # What does this do? 
##      [,1] [,2] [,3] [,4] [,5]
## [1,]    4    9   16   25   36
## [2,]    9   16   25   36   49
## [3,]   16   25   36   49   64
## [4,]   25   36   49   64   81
## [5,]   36   49   64   81  100
solve(matrix(c(1,2,3,4),nrow = 2, ncol=2)) # Inverting a matrix
##      [,1] [,2]
## [1,]   -2  1.5
## [2,]    1 -0.5

Exercises

  1. The continuous \(Uniform\left(a,b\right)\) distribution is defined on x \(\in [a,b]\) and represents a random variable that takes on any value between a and b with equal probability. It has the density function \[f\left(x\right)=\begin{cases} \frac{1}{b-a} & \;\;\;\;a\le x\le b\\ 0 & \;\;\;\;\textrm{otherwise} \end{cases}\]

    The R function dunif() evaluates this density function for the above defined values of x, a, and b. Somewhere in that function, there is a chunk of code that evaluates the density for arbitrary values of \(x\). Run this code a few times and notice sometimes the result is \(0\) and sometimes it is \(1/(10-4)=0.16666667\).

    a <- 4      # The min and max values we will use for this example
b <- 10     # Could be anything, but we need to pick something

x <- runif(n=1, 0,10)  # one random value between 0 and 10 

# what is value of f(x) at the randomly selected x value?  
dunif(x, a, b)
    ## [1] 0

    We will write a sequence of statements that utilizes if statements to appropriately calculate the density of x, assuming that a, b , and x are given to you, but your code won’t know if x is between a and b. That is, your code needs to figure out if it is and give either 1/(b-a) or 0.

    1. We could write a set of if else statements.

      a <- 4
b <- 10
x <- runif(n=1, 0,10)  # one random value between 0 and 10 

if( x < a ){
  result <- ????      # Replace ???? with something appropriate!
}else if( x <= b ){
  result <- ????
}else{
  result <- ????
}
print(paste('x=',round(x,digits=3), '  result=', round(result,digits=3)))

      Replace the ???? with the appropriate value, either 0 or \(1/\left(b-a\right)\). Run the code repeatedly until you are certain that it is calculating the correct density value. <!–

    2. We could perform the logical comparison all in one comparison. Recall that we can use & to mean “and” and | to mean “or”. In the following two code chunks, replace the ??? with either & or | to make the appropriate result.

      1. x <- runif(n=1, 0,10)  # one random value between 0 and 10 
if( (a<=x) ??? (x<=b) ){
  result <- 1/(b-a)
}else{
  result <- 0
}
print(paste('x=',round(x,digits=3), '  result=', round(result,digits=3)))
      2. x <- runif(n=1, 0,10)  # one random value between 0 and 10 
if( (x<a) ??? (b<x) ){
  result <- 0
}else{
  result <- 1/(b-a)
}
print(paste('x=',round(x,digits=3), '  result=', round(result,digits=3)))
      3. x <- runif(n=1, 0,10)  # one random value between 0 and 10 
result <- ifelse( a<=x & x<=b, ???, ??? )
print(paste('x=',round(x,digits=3), '  result=', round(result,digits=3)))
        –>

  2. I often want to repeat some section of code some number of times. For example, I might want to create a bunch plots that compare the density of a t-distribution with specified degrees of freedom to a standard normal distribution.

    library(ggplot2)
df <- 4
N <- 1000
x.grid <- seq(-4, 4, length=N)
data <- data.frame( 
  x = c(x.grid, x.grid),
  y = c(dnorm(x.grid), dt(x.grid, df)),
  type = c( rep('Normal',N), rep('T',N) ) )

# make a nice graph 
myplot <- ggplot(data, aes(x=x, y=y, color=type, linetype=type)) +
  geom_line() +
  labs(title = paste('Std Normal vs t with', df, 'degrees of freedom'))

# actually print the nice graph we made
print(myplot)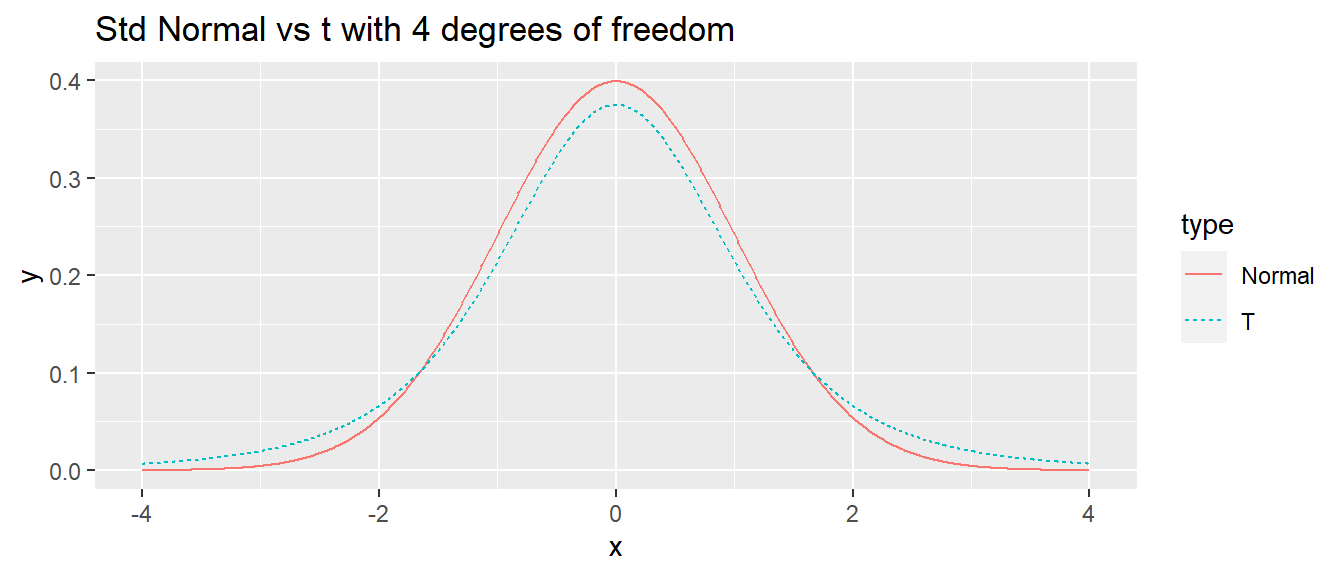

    1. Use a for loop to create similar graphs for degrees of freedom \(2,3,4,\dots,29,30\).

    2. In retrospect, perhaps we didn’t need to produce all of those. Rewrite your loop so that we only produce graphs for \(\left\{ 2,3,4,5,10,15,20,25,30\right\}\) degrees of freedom. Hint: you can just modify the vector in the for statement to include the desired degrees of freedom.

  3. It is very common to run simulation studies to estimate probabilities that are difficult to work out. In this exercise we will investigate a gambling question that sparked much of the fundamental mathematics behind the study of probability.

    The game is to roll a pair of 6-sided dice 24 times. If a “double-sixes” comes up on any of the 24 rolls, the player wins. What is the probability of winning?

    1. We can simulate rolling two 6-sided dice using the sample() function with the replace=TRUE option. Read the help file on sample() to see how to sample from the numbers \(1,2,\dots,6\). Sum those two die rolls and save it as throw.

    2. Write a for{} loop that wraps your code from part (a) and then tests if any of the throws of dice summed to 12. Read the help files for the functions any() and all(). Your code should look something like the following:

      throws <- NULL
for( i in 1:24 ){
  throws[i] <- ??????  # Your part (a) answer goes here
}
game <- any( throws == 12 ) # Gives a TRUE/FALSE value

    3. Wrap all of your code from part (b) in another for(){} loop that you run 10,000 times. Save the result of each game in a games vector that will have 10,000 elements that are either TRUE/FALSE depending on the outcome of that game. You’ll need initiallize the games vector to NULL and modify your part (b) code to save the result into some location in the vector games.

    4. Finally, calculate win percentage by taking the average of the games vector.