Chapter 7 Hypothesis Testing
Hypothesis testing is very easy to do in R. Recall that for a hypothesis test, we’re going to be testing the validity of claim about a population based on seeing some sample.
We start off with some default belief about the population, \(H_0\) which we call the Null hypothesis. We try to prove some claim about the population, \(H_1\), which we call the Alternative Hypothesis
We will say that something is statistically significant if the results are unlikely to have occurred by chance.
7.1 Exact tests and p-values
Suppose I toss a coin 10 times and I get the results H H H H H H H H T H .
As I have seen 9 heads, and one tail, it seems very unlikely that the coin is fair, but can I test this? Is the coin biased in favour of heads?
Formally, we are assuming that the probability of heads, \(p=0.5\), and finding the probability that an equally or more extreme event might occur by chance in our experiment.
We need to set our hypotheses as
\[H_0: p=0.5\] \[H_1: p\ge0.5\]
This is a one-tailed test; we could equally well have \(H_1: p\ne0.5\), but that is asking a different question (is the coin biased, as opposed to is the coin biased in favour of heads)
We need to calculate the probability that we would see nine or ten heads. We can work this out as \[\Pr(\mbox{(9H,1T) or (10H,0T)})=\Pr(\mbox{9H,1T})+\Pr(\mbox{10H,0T})\] \[={10\choose9}(0.5)^9(0.5)+{10\choose10}(0.5)^{10}=0.0107.\]
In R this is
dbinom(9,size=10,p=0.5)+dbinom(10,size=10,p=0.5)## [1] 0.01074219So the probability of this happening by chance is 0.0107. This is the p-value, and as it is less than 0.05 (which is 5%), we would reject the null hypothesis at the 5% level. We cannot reject the null hypothesis at the 1% level as our calculated value \(0.0107>0.01.\)
Remember, a p-value is the maximal significance level of the test at which we would reject the null hypothesis. It is also, by definition, the probability of obtaining a more extreme test-statistic by chance.
7.2 Testing differences in means
7.2.1 Exploring data on football
We’re going to be using a dataset on football (soccer) to illustrate our methods, available at http://www.football-data.co.uk/mmz4281/1819/E0.csv. This contains data on all the 380 Premier League matches in the 2018-2019 season. We already introduced this dataset briefly, but you can import it using the “File->Import Dataset-> From Text (readr)” menu. When importing, let’s call this data set ‘football’. You can also run the code below:
library(readr)
football <- read_csv("https://www.football-data.co.uk/mmz4281/1819/E0.csv")We’re going to test the hypothesis that teams score more goals at home than when playing away. The Full Time Goals Scored Home and Away are in the ‘FTHG’ and ‘FTAG’ columns respectively. Let’s look first at the shape of the data:
boxplot(football$FTHG,football$FTAG,names=c("Home Goals","Away Goals"))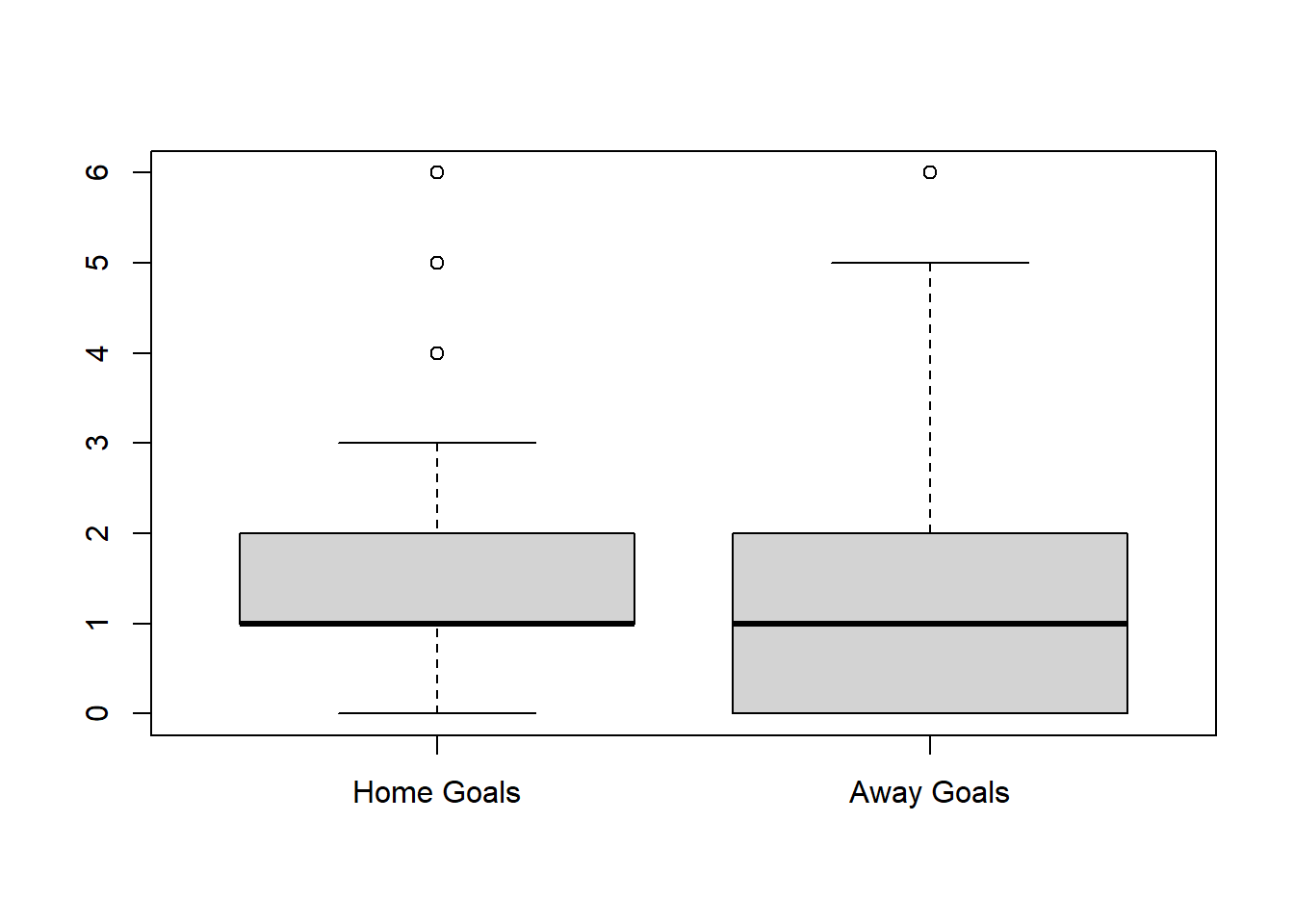
We can also look up some summary statistics of the data:
summary(football$FTHG)## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.000 1.000 1.000 1.568 2.000 6.000summary(football$FTAG)## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.000 0.000 1.000 1.253 2.000 6.000length(football$FTHG)## [1] 380This gives us the means and some other info for the Home Team’s goals, and the Away Team’s goals, and the number of games in this season (380). It certainly seems that there is a difference in the sample data, but we’ll do a hypothesis test to check this is true. ( Here we’re assuming that the goals scored in each match are determined at random from some distribution of goals and that all matches are independent- these assumptions probably aren’t true, but we’re demonstrating the computing here.)
7.2.2 Performing the test
Doing a t-test is fairly straightforward in R. Let us first assume that the variances of home and away goals is the same. All we need to do is
football.t.test<-t.test(football$FTHG,football$FTAG,var.equal = TRUE)
football.t.test##
## Two Sample t-test
##
## data: football$FTHG and football$FTAG
## t = 3.4873, df = 758, p-value = 0.000516
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## 0.1380230 0.4935559
## sample estimates:
## mean of x mean of y
## 1.568421 1.252632There’s quite a lot of information here, even for this simple test.
- Firstly, we are told that we are doing a Two Sample t-test.
- We are given the test statistics,
tof this test, and the degrees of freedom,df - We can look at the p-value here and we see that the value is incredibly small, 0.000516.
- We are told the null and alternative hypotheses for the test we are doing:
- \(H_0\) Mean Home Goals= Mean Away Goals vs
- \(H_1\) Mean Home Goals\(\ne\) Mean Away Goals i.e. this is a two-sided test. We are just testing whether the number of goals is different, rather than whether one is bigger than another.
- We are given a 95% confidence interval. We studied confidence intervals in the last chapter, and this gives you a range that we expect the true population difference between Home and Away Goals lies between. By default this is a 95% confidence interval.
- Here we can be fairly sure as both ends of the confidence interval are greater than zero (i.e. the confidence interval does not contain zero) that the number of away goals is less than the number of home goals
- Finally we are given the sample mean of this data.
The t.test output is an object like any other R object. We can examine it, and get information from the output, perhaps to put in a report. For example
names(football.t.test)## [1] "statistic" "parameter" "p.value" "conf.int" "estimate" "null.value"
## [7] "stderr" "alternative" "method" "data.name"football.t.test$estimate## mean of x mean of y
## 1.568421 1.252632football.t.test$p.value## [1] 0.0005160315What is our conclusion for this test? There are two ways of reporting the results of the hypothesis test.
- We can report the p-value. Here we see the p-value is 0.00052. This gives us a measure of the strength of evidence against our null hypothesis (formally, a p-value here is the probability of seeing a more extreme difference between the mean home and away goals occurring entirely by chance)
- We can use the p-value to report a decision based on some pre-decided significance level. For example, if we for some reason want to do a test with a 5% significance level, we can say that at the p-value is (much) less than 5%, we can reject the null hypothesis, and conclude that there is a difference between Home Goals and Away Goals.
Whether we report using the p-value of the decision-theoretic result is up to preference. The computing method is the same.
7.2.3 Customising the t-test
The dangerous thing about t-tests being so easy in R is that we don’t think about our assumptions. For example, we assumed that the variance in our football goals was the same, but is this a valid assumption? Let’s drop this assumption and see what happens:
football.t.test.2<-t.test(football$FTHG,football$FTAG,var.equal = FALSE)
football.t.test.2##
## Welch Two Sample t-test
##
## data: football$FTHG and football$FTAG
## t = 3.4873, df = 749.54, p-value = 0.0005164
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## 0.1380198 0.4935591
## sample estimates:
## mean of x mean of y
## 1.568421 1.252632Does this make a large difference in this case?
We can also change the width of the confidence level by specifying the conf.level parameter when doing the t-test. Note this doesn’t change the p-value, just how the confidence interval is displayed. Try varying this parameter.
7.2.4 One sample t-test
A simplification of the t-test is where we just with to test whether the population mean of one set of data equals a fixed value. For example, whether the mean goals scored at home \(\mu_H\) is 1.45.
t.test(football$FTHG, mu = 1.45)##
## One Sample t-test
##
## data: football$FTHG
## t = 1.7584, df = 379, p-value = 0.07949
## alternative hypothesis: true mean is not equal to 1.45
## 95 percent confidence interval:
## 1.436000 1.700842
## sample estimates:
## mean of x
## 1.568421What are the conclusions of this test?
7.2.5 One-tailed vs two tailed tests.
There are three reasonable tests we might want to do in general. In all cases we wish to test whether the mean number of home goals is 1.45, corresponding to our null hypothesis \(H_0: \mu_H=1.45\), but we have three reasonable alternative hypotheses:
- that the mean number of home goals is not 1.45, \(H_1:\mu_H\ne 1.45\)
- that the mean number of home goals is less than 1.45, \(H_1:\mu_H< 1.45\)
- that the mean number of home goals is greater than 1.45, \(H_1:\mu_H> 1.45\)
This really depends on what the claim you are trying to prove is. For example, if we know that across all football matches in the world the mean goals scored by the home team is 1.5, and we are trying to claim that the premier league is a higher scoring league, we might test the last one. Which we use depends on the claim that we are trying to assess.
t.test(football$FTHG, mu = 1.45, alternative = "two.sided") # this is the default
t.test(football$FTHG, mu = 1.45, alternative = "less")
t.test(football$FTHG, mu = 1.45, alternative = "greater")Which of these produces the smallest p-value. Does this agree with your intuition?
7.2.6 Paired t-test
One last important way of doing the t-test is where we have some natural pairing in the data and wish to incorporate it into our testing. For example, we have so far assumed that the number of goals scored in a game at home has no relationship to the away goals. This is probably an unrealistic assumption- for example, some games might be high scoring where both teams do well, or games where it rains might mean both teams score poorly. At any rate, because in this case we can identify a pairing between the home scores and the away scores, we should use a paired t-test.
football.t.test.paired<-t.test(football$FTHG,football$FTAG,
var.equal = FALSE, paired = TRUE)
football.t.test.paired##
## Paired t-test
##
## data: football$FTHG and football$FTAG
## t = 3.2143, df = 379, p-value = 0.00142
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## 0.1226151 0.5089639
## sample estimates:
## mean of the differences
## 0.3157895How does the result here compare to the unpaired equivalent?
Note we can actually find the correlation between home and away goals using R- it seems that they are negatively correlated. This might mean that if the home team is doing well, the away team has less opportunity to score- or perhaps some other reason.
cor(football$FTHG,football$FTAG)## [1] -0.1780973cor.test(football$FTHG,football$FTAG)##
## Pearson's product-moment correlation
##
## data: football$FTHG and football$FTAG
## t = -3.5189, df = 378, p-value = 0.0004862
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## -0.27379362 -0.07890933
## sample estimates:
## cor
## -0.1780973The cor.test function actually does a hypothesis test to test whether the correlation can be zero. You can see that in R a lot of the output of the testing procedures are the same, and we only need to think carefully about which test to do.
7.2.7 Another form of the t-test
The mpg dataset (in the ggplot2 library contains fuel economy data on a variety of cars. We can use it to show that there are two different formats used in the t test function (and many other hypothesis test functions in R)
library(ggplot2)
largeCars<-mpg[mpg$cyl>=6,] # Select cars with 4 or 6 cylinders.
str(largeCars)## tibble [149 x 11] (S3: tbl_df/tbl/data.frame)
## $ manufacturer: chr [1:149] "audi" "audi" "audi" "audi" ...
## $ model : chr [1:149] "a4" "a4" "a4" "a4 quattro" ...
## $ displ : num [1:149] 2.8 2.8 3.1 2.8 2.8 3.1 3.1 2.8 3.1 4.2 ...
## $ year : int [1:149] 1999 1999 2008 1999 1999 2008 2008 1999 2008 2008 ...
## $ cyl : int [1:149] 6 6 6 6 6 6 6 6 6 8 ...
## $ trans : chr [1:149] "auto(l5)" "manual(m5)" "auto(av)" "auto(l5)" ...
## $ drv : chr [1:149] "f" "f" "f" "4" ...
## $ cty : int [1:149] 16 18 18 15 17 17 15 15 17 16 ...
## $ hwy : int [1:149] 26 26 27 25 25 25 25 24 25 23 ...
## $ fl : chr [1:149] "p" "p" "p" "p" ...
## $ class : chr [1:149] "compact" "compact" "compact" "compact" ...t1<-t.test(largeCars$cty,largeCars$hwy)
t2<-t.test(cty~cyl,data = largeCars)- In the first test we just provide two sets of data
ctyandhwywe wish to compare, here to see whether the cars have different mpgs in the city and on the highway; - In the second test, ‘cty~cyl’ means we group
ctyby the variablecyl, which must have two levels for a t-test, and test whether the mean of the variablectydepends on the value ofcyl
What do we conclude from the results below?
t1##
## Welch Two Sample t-test
##
## data: largeCars$cty and largeCars$hwy
## t = -14.241, df = 239.18, p-value < 2.2e-16
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -6.692458 -5.065931
## sample estimates:
## mean of x mean of y
## 14.50336 20.38255t2##
## Welch Two Sample t-test
##
## data: cty by cyl
## t = 12.394, df = 144.17, p-value < 2.2e-16
## alternative hypothesis: true difference in means between group 6 and group 8 is not equal to 0
## 95 percent confidence interval:
## 3.062678 4.224844
## sample estimates:
## mean in group 6 mean in group 8
## 16.21519 12.571437.3 Testing for proportions
One final test we consider here is testing for proportions. For example, we may toss a coin 100 times and get 45 heads. We might ask ourselves the question whether the coin is fair or not. Formally, we are testing letting X be a binomial random variable with \(n=100\) trials, and testing the hypotheses
- \(H_0\): The proportion of heads, p, is 0.5 (p=0.5) vs
- \(H_1\): The proportion of heads, p, is not 0.5.
This is a two sided hypothesis test for proportion, based on seeing data \(x=45\). In R this is straightforward:
prop.test(x=45, n=100, p=0.50, conf.level=0.99)##
## 1-sample proportions test with continuity correction
##
## data: 45 out of 100, null probability 0.5
## X-squared = 0.81, df = 1, p-value = 0.3681
## alternative hypothesis: true p is not equal to 0.5
## 99 percent confidence interval:
## 0.3244114 0.5820457
## sample estimates:
## p
## 0.45As our p-value is high, we can conclude that there is no evidence that the coin is biased, and we get a confidence interval for the true value of the probability of heads, \(p\).
We can also apply this test to data directly. For example, if we want to test whether the proportion of wins by the Home Team is equal to 40%, we can count the number of home wins in football, and test that directly
wins<-sum(football$FTR=="H")
prop.test(x=wins,n=380,p=0.4)##
## 1-sample proportions test with continuity correction
##
## data: wins out of 380, null probability 0.4
## X-squared = 8.9062, df = 1, p-value = 0.002842
## alternative hypothesis: true p is not equal to 0.4
## 95 percent confidence interval:
## 0.4252923 0.5278257
## sample estimates:
## p
## 0.4763158We can also test whether there is a difference between two proportions. If we wish to test whether
x1<-sum((football$FTR=="H")&(football$HomeTeam=="Arsenal"))# Number of Home Wins by Arsenal
x2<-sum((football$FTR=="H")&(football$HomeTeam=="Chelsea")) # Number of Home Wins by Chelsea
prop.test(x = c(x1, x2), n = c(19, 19), alternative = "greater")##
## 2-sample test for equality of proportions with continuity correction
##
## data: c(x1, x2) out of c(19, 19)
## X-squared = 0.12179, df = 1, p-value = 0.3635
## alternative hypothesis: greater
## 95 percent confidence interval:
## -0.1938345 1.0000000
## sample estimates:
## prop 1 prop 2
## 0.7368421 0.6315789This shows that there is no evidence that Arsenal win at home more often than Chelsea, based on our limited sample of 19 home games for each team. We get a confidence interval for the differences in proportions of Home Wins. How should we interpret this?
7.4 Exercises
- The built in data set
sleepcontains information on the effect of two soporific drugs on 10 patients.- Present box plots of the data showing the difference between the two groups (the two drugs).
- Perform an (unpaired) t-test to see whether the effect of the drugs is different between the groups.
- In fact, the groups variable is perhaps misnamed: the same 10 patients were given each drug. Repeat the t-test for paired data. Does it change your conclusion?
*Hint: Looking up the help file for the sleep data will tell you a lot about this data set
- The
birthwtdata in theMASSlibrary provides data on the Risk Factors Associated with Low Infant Birth Weight.- Produce a box plot of the birth weight for each smoking status of the mother. Does it look like there is a difference in birth weights depending on the smoking status?
- Test the hypothesis that there is a relationship between smoking and a lower birth weight.
- The column ‘low’ indicates whether the birth weight is considered low. Use an appropriate test to see whether there is an association between the birth weight and the smoking status. How does this compare with your test in part b?
- For the football dataset, test the following hypotheses:
- The number of total goals scored in a game was higher in the second half of the games than in the first half of the game.
- The proportion of games in which a yellow card was given to the home team was lower than the proportion of games in which a yellow card was given to an away team (the number of cards in a game are stored in the
HYandAYcolumns)