OR-Notes are a series of introductory notes on topics that fall under the broad heading of the field of operations research (OR). They were originally used by me in an introductory OR course I give at Imperial College. They are now available for use by any students and teachers interested in OR subject to the following conditions.
A full list of the topics available in OR-Notes can be found here.
When formulating LP's we often found that, strictly, certain variables should have been regarded as taking integer values but, for the sake of convenience, we let them take fractional values reasoning that the variables were likely to be so large that any fractional part could be neglected. Whilst this is acceptable in some situations, in many cases it is not, and in such cases we must find a numeric solution in which the variables take integer values.
Problems in which this is the case are called integer programs (IP's) and the subject of solving such programs is called integer programming (also referred to by the initials IP).
IP's occur frequently because many decisions are essentially discrete (such as yes/no, go/no-go) in that one (or more) options must be chosen from a finite set of alternatives.
Note here that problems in which some variables can take only integer values and some variables can take fractional values are called mixed-integer programs (MIP's).
As for formulating LP's the key to formulating IP's is practice. Although there are a number of standard "tricks" available to cope with situations that often arise in formulating IP's it is probably true to say that formulating IP's is a much harder task than formulating LP's.
We consider an example integer program below.
There are four possible projects, which each run for 3 years and have the following characteristics.
Capital requirements (£m) Project Return (£m) Year 1 2 3 1 0.2 0.5 0.3 0.2 2 0.3 1.0 0.8 0.2 3 0.5 1.5 1.5 0.3 4 0.1 0.1 0.4 0.1 Available capital (£m) 3.1 2.5 0.4
We have a decision problem here: Which projects would you choose in order to maximise the total return?
We follow the same approach as we used for formulating LP's - namely:
We do this below and note here that the only significant change in formulating IP's as opposed to formulating LP's is in the definition of the variables.
Here we are trying to decide whether to undertake a project or not (a "go/no-go" decision). One "trick" in formulating IP's is to introduce variables which take the integer values 0 or 1 and represent binary decisions (e.g. do a project or not do a project) with typically:
Such variables are often called zero-one or binary variables
To define the variables we use the verbal description of
xj = 1 if we decide to do project j (j=1,...,4) = 0 otherwise, i.e. not do project j (j=1,...,4)
Note here that, by definition, the xj are integer variables which must take one of two possible values (zero or one).
The constraints relating to the availability of capital funds each year are
0.5x1 + 1.0x2 + 1.5x3 + 0.1x4
<= 3.1 (year 1)
0.3x1 + 0.8x2 + 1.5x3 + 0.4x4
<= 2.5 (year 2)
0.2x1 + 0.2x2 + 0.3x3 + 0.1x4
<= 0.4 (year 3)
To maximise the total return - hence we have
maximise 0.2x1 + 0.3x2 + 0.5x3 + 0.1x4
This gives us the complete IP which we write as
maximise 0.2x1 + 0.3x2 + 0.5x3 + 0.1x4
subject to
0.5x1 + 1.0x2 + 1.5x3 + 0.1x4
<= 3.1
0.3x1 + 0.8x2 + 1.5x3 + 0.4x4
<= 2.5
0.2x1 + 0.2x2 + 0.3x3 + 0.1x4
<= 0.4
xj = 0 or 1 j=1,...,4
Note:
Extensions to this basic problem include:
How to amend our basic IP to deal with such extensions is given here.
In fact note here that integer programming/quantitative modelling techniques are increasingly being used for financial problems.
For solving LP's we have general purpose (independent of the LP being solved) and computationally effective (able to solve large LP's) algorithms (simplex or interior point).
For solving IP's no similar general purpose and computationally effective algorithms exist.
Indeed theory suggests that no general purpose computationally effective algorithms will ever be found. This area is known as computational complexity and concerns NP-completeness. It was developed from the early 1970's onward and basically is a theory concerning "how long it takes algorithms to run". This means that IP's are a lot harder to solve than LP's.
Solution methods for IP's can be categorised as:
Solution methods for IP's can also be categorised as:
An optimal algorithm is one which (mathematically) guarantees to find the optimal solution.
It may be that we are not interested in the optimal solution:
In such cases we can use a heuristic algorithm - that is an algorithm that should hopefully find a feasible solution which, in objective function terms, is close to the optimal solution. In fact it is often the case that a well-designed heuristic algorithm can give good quality (near-optimal) results.
For example a heuristic for our capital budgeting problem would be:
Applying this heuristic we would choose to do just project 1 and project 2, giving a total return of 0.5, which may (or may not) be the optimal solution.
Hence we have four categories that we potentially need to consider:
Note here that the methods presented below are suitable for solving both IP's (all variables integer) and MIP's (mixed-integer programs - some variables integer, some variables allowed to take fractional values).
We shall deal with just two general purpose (able to deal with any IP) optimal solution algorithms for IP's:
We consider each of these in turn below. Note here that there does exist another general purpose solution algorithm based upon cutting planes but this is beyond the scope of this course.
Unlike LP (where variables took continuous values (>=0)) in IP's (where all variables are integers) each variable can only take a finite number of discrete (integer) values.
Hence the obvious solution approach is simply to enumerate all these possibilities - calculating the value of the objective function at each one and choosing the (feasible) one with the optimal value.
For example for the capital budgeting problem considered above there are 24=16 possible solutions. These are:
x1 x2 x3 x4 0 0 0 0 do no projects 0 0 0 1 do one project 0 0 1 0 0 1 0 0 1 0 0 0 0 0 1 1 do two projects 0 1 0 1 1 0 0 1 0 1 1 0 1 0 1 0 1 1 0 0 1 1 1 0 do three projects 1 1 0 1 1 0 1 1 0 1 1 1 1 1 1 1 do four projects
Hence for our example we merely have to examine 16 possibilities before we know precisely what the best possible solution is. This example illustrates a general truth about integer programming:
What makes solving the problem easy when it is small is precisely what makes it become very hard very quickly as the problem size increases
This is simply illustrated: suppose we have 100 integer variables each with 2 possible integer values then there are 2x2x2x ... x2 = 2100 (approximately 1030) possibilities which we have to enumerate (obviously many of these possibilities will be infeasible, but until we generate one we cannot check it against the constraints to see if it is feasible or not).
This number is plainly too many for this approach to solving IP's to be computationally practicable. To see this consider the fact that the universe is around 1010 years old so we would need to have considered 1020 possibilities per year, approximately 4x1012 possibilities per second, to have solved such a problem by now if we started at the beginning of the universe.
Be clear here - conceptually there is not a problem - simply enumerate all possibilities and choose the best one. But computationally (numerically) this is just impossible.
IP nowadays is often called "combinatorial optimisation" indicating that we are dealing with optimisation problems with an extremely large (combinatorial) increase in the number of possible solutions as the problem size increases.
The most effective general purpose optimal algorithm is LP-based tree search (tree search also being called branch and bound). This is a way of systematically enumerating feasible solutions such that the optimal integer solution is found.
Where this method differs from the enumeration method is that not all the feasible solutions are enumerated but only a fraction (hopefully a small fraction) of them. However we can still guarantee that we will find the optimal integer solution. The method was first put forward in the early 1960's by Land and Doig.
Consider our example capital budgeting problem. What made this problem difficult was the fact that the variables were restricted to be integers (zero or one). If the variables had been allowed to be fractional (takes all values between zero and one for example) then we would have had an LP which we could easily solve. Suppose that we were to solve this LP relaxation of the problem [replace xj = 0 or 1 j=1,...,4 by 0 <= xj <= 1 j=1,...,4]. Then using the package we get x2=0.5, x3=1, x1=x4=0 of value 0.65 (i.e. the objective function value of the optimal linear programming solution is 0.65).
As a result of this we now know something about the optimal integer solution, namely that it is <= 0.65, i.e. this value of 0.65 is a (upper) bound on the optimal integer solution. This is because when we relax the integrality constraint we (as we are maximising) end up with a solution value at least that of the optimal integer solution (and maybe better).
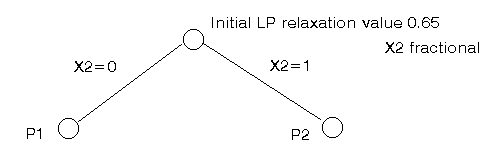
Consider this LP relaxation solution. We have a variable x2 which is fractional when we need it to be integer. How can we rid ourselves of this troublesome fractional value? To remove this troublesome fractional value we can generate two new problems:
then we will claim that the optimal integer solution to the original problem is contained in one of these two new problems. This process of taking a fractional variable (a variable which takes a fractional value in the LP relaxation) and explicitly constraining it to each of its integer values is known as branching. It can be represented diagrammatically as below (in a tree diagram, which is how the name tree search arises).

We now have two new LP relaxations to solve. If we do this we get:
This can be represented diagrammatically as below.

To find the optimal integer solution we just repeat the process, choosing one of these two problems, choosing one fractional variable and generating two new problems to solve.
Choosing problem P1 we branch on x1 to get our list of LP relaxations as:
This can again be represented diagrammatically as below.
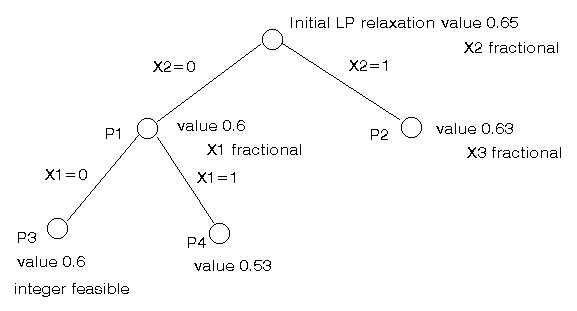
At this stage we have identified a integer feasible solution of value 0.6 at P3. There are no fractional variables so no branching is necessary and P3 can be dropped from our list of LP relaxations.
Hence we now have new information about our optimal (best) integer solution, namely that it lies between 0.6 and 0.65 (inclusive).
Consider P4, it has value 0.53 and has a fractional variable (x3). However if we were to branch on x3 any objective function solution values we get after branching can never be better (higher) than 0.53. As we already have an integer feasible solution of value 0.6 P4 can be dropped from our list of LP relaxations since branching from it could never find an improved feasible solution. This is known as bounding - using a known feasible solution to identify that some relaxations are not of any interest and can be discarded.
Hence we are just left with:
Branching on x3 we get
Neither of P5 or P6 lead to further branching so we are done, we have discovered the optimal integer solution of value 0.6 corresponding to x3=x4=1, x1=x2=0.
The entire process we have gone through to discover this optimal solution (and to prove that it is optimal) is shown graphically below.
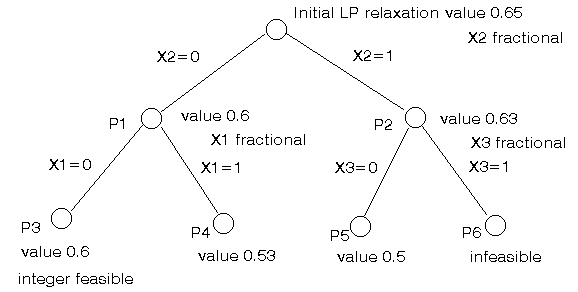
You should be clear as to why 0.6 is the optimal integer solution for this problem, simply put if there were a better integer solution the above tree search process would (logically) have found it.
Note here that this method, like complete enumeration, also involves powers of two as we progress down the (binary) tree. However also note that we did not enumerate all possible integer solutions (of which there are 16). Instead here we solved 7 LP's. This is an important point, and indeed why tree search works at all. We do not need to examine as many LP's as there are possible solutions. Whilst the computational efficiency of tree search differs for different problems it is this basic fact that enables us to solve problems that would be completely beyond us were we to try complete enumeration.
You may have noticed that in the example above we never had more than one fractional variable in the LP solution at any tree node. This arises due to the fact that in constructing the above example I decided to make the situation as simple as possible. In general we might well have more than one fractional variable at a tree node and so we face a decision as to which variable to choose to branch on. A simple rule for deciding might be to take the fractional variable which is closest in value to 0.5, on the basis that the two branches (setting this variable to zero and one respectively) may well perturb the situation significantly.
Good computer packages (solvers) exist for finding optimal solutions to IP's/MIP's via LP-based tree search. Many of the computational advances in IP optimal solution methods (e.g. constraint aggregation, coefficient reduction, problem reduction, automatic generation of valid inequalities) are included in these packages. Often the key to making successful use of such packages for any particular problem is to put effort into a good formulation of the problem in terms of the variables and constraints. By this we mean that for any particular IP there may be a number of valid formulations. Deciding which formulation to adopt in a solution algorithm is often a combination of experience and trial and error.
Constraint logic programming (CLP), also called constraint programming, which is essentially branch and bound but without the bound, can be of use here if:
Currently there is a convergence between CLP and LP-based solvers with ILOG and CPLEX merging.
The branch and bound method is the method used by the package. If you do not have access to an integer programming package one package (albeit with restricted capacity) is available free here.
The package input for the problem presented above is given below.
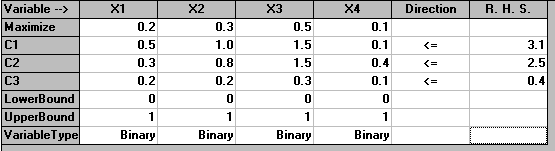
with the solution being shown below.

Here we can see that the optimal decision is to choose to do projects 3 and 4.
Capital budgeting solution - using Solver
Below we solve the capital budgeting problem with the Solver add-in that comes with Microsoft Excel.
If you click here you will be able to download an Excel spreadsheet called ip.xls that already has the IP we are considering set up.
Take this spreadsheet and look at Sheet A. You should see the problem we considered above set out as:
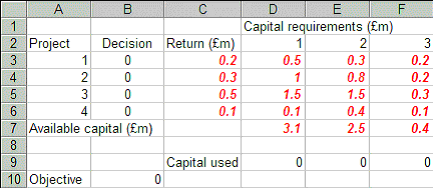
Here we have set up the problem with the decisions (the zero-one variables) being shown in cells B3 to B6. The capital used in each of the three years is shown in cells D9 to F9 and the objective (total return) is shown in cell B10 (for those of you interested in Excel we have used SUMPRODUCT in cells D9 to F9 and B10 as a convenient way of computing the sum of the product of two sets of cells).
Doing Tools and then Solver you will see:
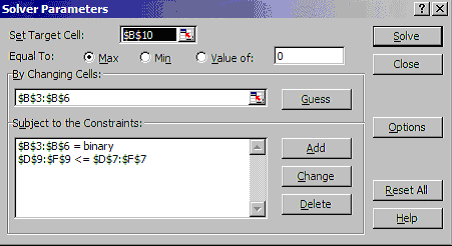
where B10 is to be maximised (ignore the use of $ signs here - that is a technical Excel issue if you want to go into it in greater detail) by changing the decision cells B3 to B6 subject to the constraints that these cells have to be binary (zero-one) and that D9 to F9 are less than or equal to D7 to F7, the capital availability constraints.
Clicking on Options on the above Solver Parameters box you will see:

showing that we have ticked Assume Linear Model and Assume Non-Negative.
Solving we get:
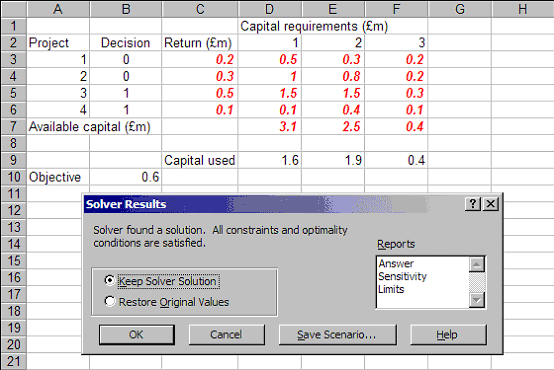
indicating that the optimal decision (the decision that achieves the maximum return of 0.6 shown in cell B10) is to do projects 3 and 4 (the decision variables are one in cells B5 and B6, but not to do projects 1 and 2 (the decision variables are zero in cells B3 and B4).
I will mention in the lecture (if there is time) a number of IP problems I have been involved with:
Essentially the only effective approach here is to run a general purpose optimal algorithm and terminate early (e.g. after a specified computer time).
If we are dealing with one specific type of IP then we might well be able to develop a special purpose solution algorithm (designed for just this one type of IP) that is more effective computationally than the general purpose branch and bound method given earlier. These are typically tree search approaches based upon generating bounds via:
Such algorithms, being different for different problems, are really beyond the scope of this course but suffice to say:
A large amount of academic effort in this field is devoted to generating methods that out-perform previous methods for the same problem.
On a personal note this is an area with which I am familiar and special purpose algorithms can be very effective (e.g. a problem dealing with the location of warehouses and involving some 500,000 continuous variables, 500 zero-one variables and 500,000 constraints solved in some 20 minutes). They can be very successful compared with general purpose optimal algorithms (perhaps an order of magnitude or more in terms of the size of problem that can be solved).
You should be clear though why a special purpose optimal algorithm can be so computationally more effective than a general purpose optimal algorithm, it is because you have to put intellectual effort into designing the algorithm!
With regard to heuristics we have a number of generic approaches in the literature, for example:
By generic here we mean that there is a general framework/approach from which to build an algorithm. All of these generic approaches however must be tailored for the particular IP we are considering. In addition we can design heuristics purely for the particular problem we are considering (problem-specific heuristics).
Heuristics for IP's are widespread in the literature and applied quite widely in practice. Less has been reported though in terms of heuristics for MIP's.
More about heuristics can be found here.
There are many areas in which IP has been applied, below we briefly mention some of them, but only in words, no more maths!
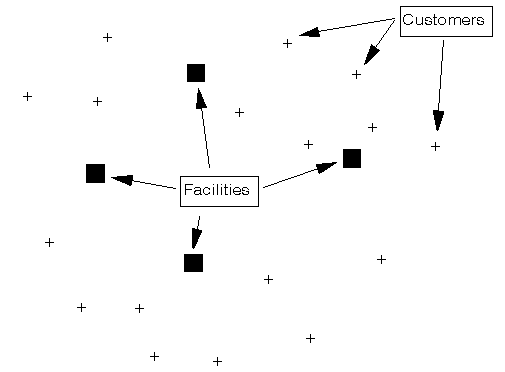
Given a set of facility locations and a set of customers who are served from the facilities then:
Typically here facilities are regarded as "open" (used to serve at least one customer) or "closed" and there is a fixed cost which is incurred if a facility is open. Which facilities to have open and which closed is our decision (hence an IP with a zero-one variable representing whether the facility is closed (zero) or open (one)).
Below we show a graphical representation of the problem.
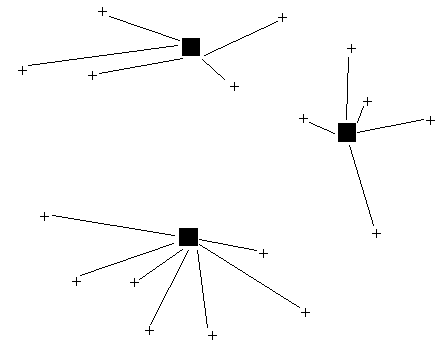
One possible solution is shown below.
Other factors often encountered here:
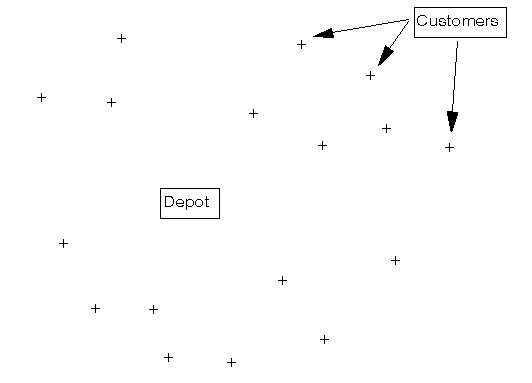
Given a set of vehicles based at a central depot and a set of geographically dispersed customers which require visits from the vehicles (e.g. to supply some goods) which vehicles should visit which customers and in what order?
The problem is shown graphically below.
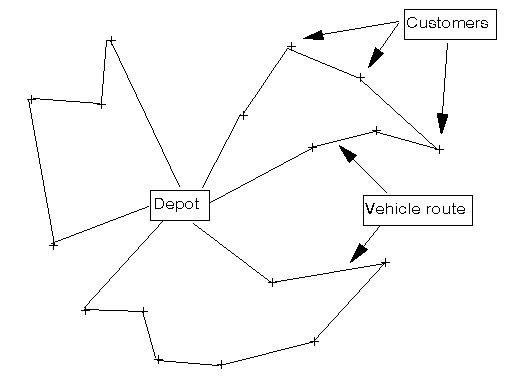
One possible solution is:
Other factors that can occur here are:
For more about this problem see the vehicle routing notes.
As a final thought, any decision problem where any of the decisions that have to be made are essentially discrete (such as yes/no, go/no-go), in that one option must be chosen from a finite set of alternatives, can potentially be formulated and solved as an integer programming problem.
Recall the four categories we had:
One point to note here, although we did not stress it above, is that often an heuristic algorithm can be built for an IP problem without ever having a mathematical formulation of the problem. After all one starts from a verbal description of a problem to construct a mathematical formulation, equally one can construct (i.e. design and code) a heuristic algorithm from a verbal description of the problem (e.g. see here to see an example of this).
Factors which come into play in choosing which IP solution method is appropriate are:
Note too that typically IP is used (if applicable) when: