OR-Notes are a series of introductory notes on topics that fall under the broad heading of the field of operations research (OR). They were originally used by me in an introductory OR course I give at Imperial College. They are now available for use by any students and teachers interested in OR subject to the following conditions.
A full list of the topics available in OR-Notes can be found here.
The approach we follow in dealing with network flow is not common in the textbooks. Essentially we adopt a unified approach to a number of different problems whereas most of the textbooks (for historical reasons) treat these problems separately.
We shall first consider the general network flow problem and then show how a number of common practical problems are variants of this general problem.
To illustrate the general network flow problem consider the diagram below where we have a number of sources of material and a number of sinks (or demand points) for material. Typically each source has an upper limit on the amount of material it can supply and each demand point has an associated number indicating the amount of material it needs.
Between the sources and the sinks are intermediate nodes through which material can be shipped (flows) to other intermediate nodes or to the sinks. We also have arcs (essentially directed from the sources to the sinks) where each arc has associated with it:
Hence the problem is one of deciding how to supply the sinks from the sources at minimum cost. This problem is known as the minimum cost network flow problem.
Ford and Fulkerson developed an algorithm (called the "out of kilter" algorithm) for this problem in the early 1960's and this original algorithm has been revised and improved since then. Algorithms for minimum cost network flow are widely available on computers. The minimum cost network flow problem is a linear program with a special structure. As such specialised algorithms can solve very large problems.
Any problem which can be represented in the form of a picture such as shown above can be regarded as a minimum cost network flow problem (and hence easily solved).
Below we consider the practical problems which can be regarded as minimum cost network flow problems.
Consider the table below which shows the cost of allocating 5 jobs to 5 machines.
Machine
A B C D E
Job 1 22 30 26 16 25
2 27 29 28 20 32
3 33 25 21 29 23
4 24 24 30 19 26
5 30 33 32 37 31
Which jobs should be allocated to which machines so as to minimise the total cost?
It is clear that this problem can be viewed as a minimum cost network flow problem as below where:
Problems of this type are called assignment problems since they involve the assignment of n (in this case n=5) distinct entities to another n distinct entities. For example in the area of production planning we might be interested in assigning operators to machines, or in assigning operators to jobs, or (as above) in assigning jobs to machines.
This problem was solved using the package, the input being shown below.
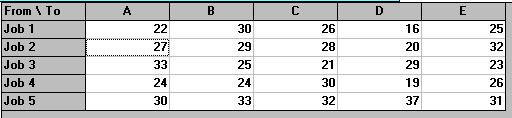
The output is shown below.
Three factories can supply any of six customers with a particular product. The demand for this product from each of the customers 1, 2, 3, 4, 5 and 6 is 40, 35, 25, 20, 60 and 30 tons respectively. Maximum production at factories A, B and C is 60, 70 and 80 tons respectively. The variable production cost per ton is 11.3, 11.0 and 10.8 (£) at factories A, B and C respectively and the transportation cost per ton from each factory to each customer is as shown below.
Transportation cost (£)
per ton to customer
1 2 3 4 5 6
From factory A 1.5 1.8 3.1 4.2 2.5 3.0
B 2.2 4.6 3.5 2.4 1.8 4.0
C 3.6 4.8 1.6 4.4 2.8 2.0
Determine the quantity of product to be supplied from each factory to each customer so as to minimise total costs.
In order to treat this problem as a minimum cost network flow problem we need first to find the cost for each factory/customer pair of producing and transporting one ton from the factory to the customer. These costs are obtained by adding the variable production costs to the transportation costs and are tabulated below.
Production and transportation
cost (£) per ton to customer
1 2 3 4 5 6
From factory A 12.8 13.1 14.4 15.5 13.8 14.3
B 13.2 15.6 14.5 13.4 12.8 15.0
C 14.4 15.6 12.4 15.2 13.6 12.8
It is now clear that this problem can be viewed as a minimum cost network flow problem as below where:
Problems of this type are called transportation problems and typically involve minimising the cost of transporting goods from production facilities to customers.
Note here that:
This problem was solved using the package, the input being shown below.
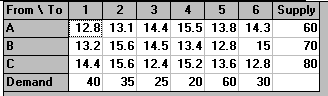
The output is shown below.
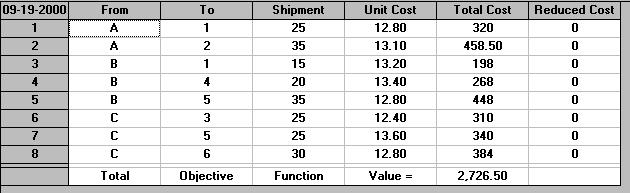
Note here that customer 1 receives shipments from both A and B. This is normal in solving transportation problems. If we wish each customer to be sourced (supplied) from just a single factory then the problem becomes a much more difficult problem (in fact it becomes an integer programming problem).
Frequently goods are not transported directly from factories to customers but are shipped (transhipped) via intermediate locations (such as depots or warehouses). For example suppose we take the problem we considered above and add the additional information that a new depot has become available where:
This depot can be incorporated into the network flow representation as below .
Here we have added to the graph shown before:
Problems of this type are called transhipment problems since they involve the transhipment of goods via intermediate locations rather than directly from factories to customers.
This problem was solved using the package. The input is shown below. Note here that this problem is entered as a network flow problem.

The output is shown below.
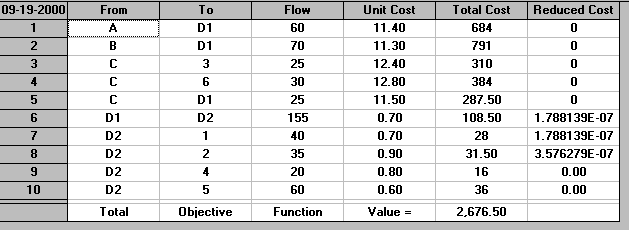
It can be seen that 155 units flows through the depot (from D1 to D2). If we (for example) restrict that to say 100 units (because the depot cannot cope with more than that) we merely need to edit the Flows Bounds in the package appropriately. The solution with this capacity limit imposed is shown below.
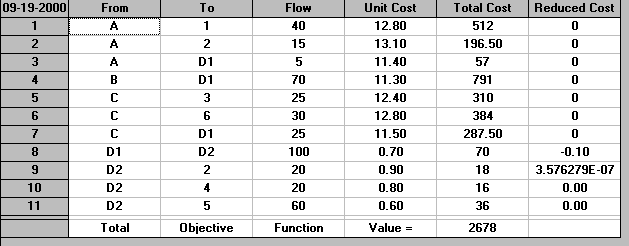
As both the transportation and transhipment problems are (computationally) easy to solve "what-if" questions can be asked and answered relatively rapidly, both at the strategic level and at the tactical level. For example:
Increasing factory capacity is a strategic decision and presumably an increase in factory capacity reduces the variable costs involved in production and transportation. Hence this variable cost reduction should be set against the capital required to increase the factory capacity (a typical investment decision, balance cost savings against capital investment)
Both the transportation problem and the transhipment problem are quite widely used for planning bulk distribution, especially in the USA where the (road) distances travelled are large.
A variation on the general minimum cost network flow problem is the problem of finding the maximum flow that can be sent between a single source and a single sink (as in the diagram below) where each arc has a capacity (shown in the diagram below next to the arc) which limits the amount of flow which can be sent down it (there being no cost associated with using the arc).
An algorithm for solving this problem was developed by Ford and Fulkerson in the mid 1950's (i.e. before they developed their "out of kilter" algorithm for solving the minimum cost network flow problem). Problems of this type are called maximum flow problems and appear, for example, in communication network planning and pipeline (gas/oil/water) network planning.
The problem shown above was solved using the package, the input being shown below.
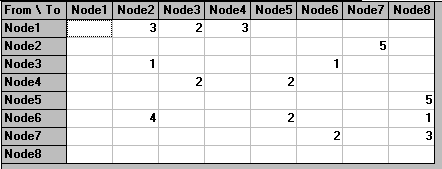
The output is shown below.
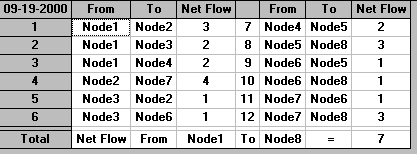
We can see from that output that the maximum flow that can be sent between the source and the sink is 7.
Note here that there is a theorem (the min-cut max-flow theorem) that says that the maximum flow possible is equal to the capacity of the minimum cut disconnecting the source and the sink (i.e. a cut that disconnects source and sink and has the minimum (smallest) possible capacity over all such cuts). In the above problem the min-cut corresponds to the arcs (1,2), (3,2), (3,6) and (4,5) - removing these disconnects the source and the sink (see below) and their total capacity is 7.
One other area in which network flow is extensively used is in the management of foreign exchange dealings for banks, large companies, etc. To illustrate this consider the (simple) problem shown below where there are 4 currencies (£, Swiss franc, US dollar and Japanese Yen).
On the international money market rates are constantly available for converting between any pair of these (commonly traded) currencies and these rates can be represented by the matrix (rij) where
rij = the amount of currency j obtained in return for one unit of currency i
For example the amount of Yen (currency 4) obtained in return for one £ (currency 1) is r14.
Consider first a simple deal in which we convert one £ to Yen and back again. We will end up with £[r14(r41)] (ignoring transaction costs). The key point is that almost always r14(r41) is not equal to 1. This arises principally because rates are only quoted to a certain number of decimal places.
Whilst we would expect r14(r41) < 1 (i.e. we lose money on the deal) it is not so clear that a deal representing a complex series of transactions will necessarily be unprofitable (e.g. would converting one £ to US dollars to Swiss francs to Yen to £ - yielding £[r13r32r24r41 ] necessarily be unprofitable?)
In fact, given that a large number of currencies are commonly traded, that rapid changes in rates occur, that rates are decided by people and are quoted to a certain number of decimal places it is almost inevitable that profitable deals can (occasionally) be found.
Foreign exchange transactions (such as those above) can be modelled as a network flow with gains problem and algorithms exist which enable profitable deals to be identified within seconds (necessary when rates are constantly changing). Note too the number of currencies that are commonly traded, think of the major trading blocs around the world for example:
Whilst the above has considered just the spot market (converting currency immediately) the same basic approach can be extended to have a time dimension, including both the forward market (converting currency at a given point in the future) and deposits (depositing currency for a certain time to gain interest).
To include the time dimension we simply repeat the same picture shown above for each time period and then we have that the arcs between currency nodes in different time periods naturally represent forward transactions and deposits. This is shown below.
Note that there can be two types of arcs in the above problem:
For example a risk-free arc might be investing £ in the current time period (period 1) for a fixed time in an fixed interest instrument (issued by a reputable issuer). A risky arc might be changing money on the spot market in period 2 (as we do not yet know what the spot market rate in period 2 will be). Apart from pure "speculation" to make money, such models can be used, for example, to balance the currency holdings of a company so as to meet its future requirements for foreign currency at minimum cost.
Note here that problems concerned with the management of foreign exchange are often referred to as arbitrage problems.
Note too that the opportunities for profitable speculation diminish as more and more players in the foreign exchange market have powerful computers and sophisticated software at their fingertips.
Commercial computer codes for the minimum cost network flow problem are readily available and able to solve large problems. In solving such problems it is the number of arcs which (essentially) determines the solution time.
Computational results presented in the literature indicate that problems involving thousands of arcs can be solved within seconds (on a powerful computer).
For example I have solved transportation problems involving 10 sources and 1000 demand points (10,000 arcs) in about 5 seconds.