OR-Notes are a series of introductory notes on topics that fall under the broad heading of the field of operations research (OR). They were originally used by me in an introductory OR course I give at Imperial College. They are now available for use by any students and teachers interested in OR subject to the following conditions.
A full list of the topics available in OR-Notes can be found here.
One important extension to the basic network analysis technique relates to project cost/ project time tradeoff.
In this extension to the basic method we assume that, for each activity, the completion time can be reduced (within limits) by spending more money on the activity. Essentially each activity now has more than one possible completion time (depending upon how much money we are willing to spend on it).
This use of cost information is the CPM technique.
A common assumption is to say that for each activity the completion time can lie in a range with a linear relationship holding between cost and activity completion time within this range (as illustrated below).
Reducing an activity completion time is known as "crashing" the activity and to illustrate this concept consider the activity on node network we had before, for which the network diagram is reproduced below.
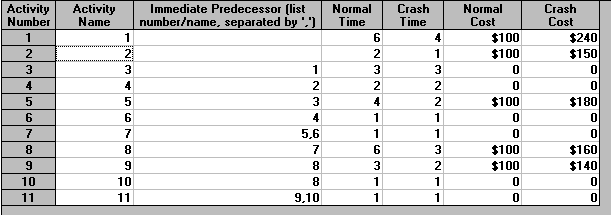
Introducing costs into this problem we have the package input shown below. For activity 1, for example, the normal cost is 100 associated with a normal time of 6 weeks, and the crash cost is 240 associated with a crash time of 4 weeks.
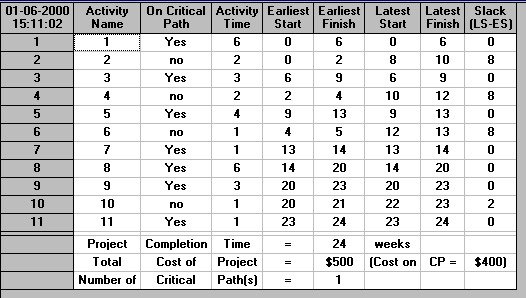
The output from the package for this example is shown below.
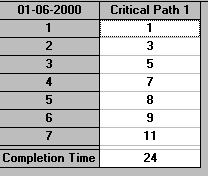
The above calculation is based upon the normal times for each activity. If we were to adopt the crash times for each and every activity we would have:

indicating that the project can take anywhere between 24 and 16 weeks depending upon the activity completion time (which can vary between the normal time and the crash time).
As seen above we can have any possible project completion time between 24 and 16 weeks - but which one shall we choose? To help us answer this question let us first consider 23 weeks, i.e. we wish to move from the normal time project duration of 24 weeks to a project duration of 23 weeks. Plainly to achieve a project completion time of 23 weeks this we need to crash (reduce) the completion time of one (or more) activities - but which ones?
The solution associated with 24 weeks has one critical path, namely 1-3-5-7-8-9-11. Clearly unless we crash an activity on this critical path we can never reduce the completion time of the entire project. Of these activities only 1, 5, 8 and 9 are capable of being crashed:
Clearly the best choice is to crash the activity with the lowest incremental (additional) cost - so in this case we would choose to crash activity 8 by one week at an additional cost of 20. This will reduce the length (duration) of the critical path 1-3-5-7-8-9-11 by one week, i.e. from 24 weeks to 23 weeks.
The new situation is:
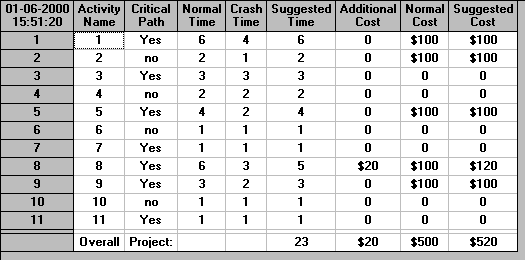

Suppose now we wish to reduce the project by a further week, i.e. to 22 weeks. Plainly we will adopt the same approach as before:
This procedure works perfectly until we reach a situation in which there are two or more critical paths. In such cases the activity with the lowest incremental cost may not be the best choice.
For example if there are two critical paths A-E-F and B-E-F in a network and activity A has the lowest incremental cost then crashing activity A will have no effect on the critical path B-E-F, and hence no effect on the overall project completion time. We would still need to crash one activity on B-E-F before we could reduce the completion time for the entire project. In fact in this situation we would need to consider three options:
to determine the best approach. Clearly once there is more than one critical path the situation becomes more complicated. Indeed we stressed the word perfectly above. More technically, choosing to crash the critical activity with the lowest incremental cost is guaranteed to be an optimal approach (i.e. we crash in the best possible way) provided we have only a single critical path. However once we encounter two or more critical paths we cannot guarantee that we can still crash the project in an optimal way.
Returning for the moment to our network above the solution associated with 23 weeks has one critical path, namely 1-3-5-7-8-9-11, as before. Of these activities only 1, 5, 8 and 9 are capable of being crashed
Clearly the best choice is to crash the activity with the lowest incremental (additional) cost - so in this case we would choose to crash activity 8 by one week at an additional cost of 20. This will reduce the length (duration) of the critical path 1-3-5-7-8-9-11 by one week, i.e. from 23 weeks to 22 weeks.
Hence we could continue as above, and eventually we would have crashed the network down to its lowest possible completion time of 16 weeks.
Whilst you might expect that the package would crash the project in the same manner as considered above (look at incremental costs) in fact it uses a totally different approach. The package calculates the optimal (minimum cost) way to crash the project using linear programming. As discussed previously we can formulate a network problem using linear programming. This formulation can be easily modified to deal with the problem of crashing (as will be seen later below).
The advantage of using linear programming to crash a project is that we can automatically guarantee that, for any particular project completion time, we have achieved that time by crashing in a minimum cost fashion. Crashing using incremental costs may, because of the difficulty of dealing with multiple critical paths, not lead us to a minimum cost solution for each possible project completion time.
The package output giving the cost associated with crashing the project from its normal completion time of 24 weeks to 19 weeks (for example) is given below.
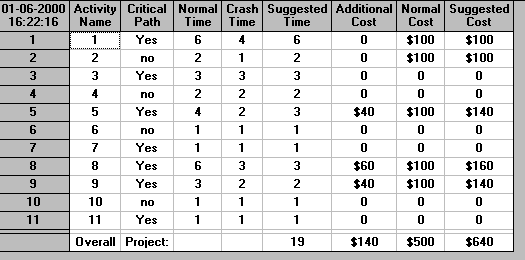
It can be seen that the minimum cost way to achieve an overall project completion time of 19 weeks is by crashing activity 5 by one week, activity 8 by three weeks and activity 9 by one week.
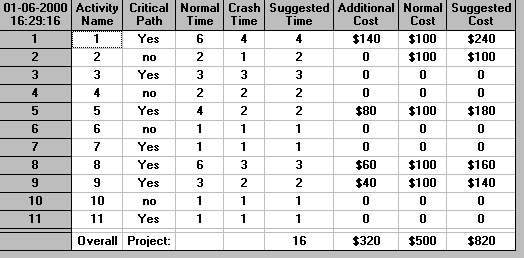
The output below shows the minimum cost way of achieving the lowest possible overall project completion time of 16 weeks. It can be seen that this can be done for a cost of 820. This contrasts with the cost of 870 associated with using all activities at their crash times. The difference arises because it is not necessary to crash all activities to their maximum extent to achieve an overall project completion time of 16 (in this case activity 2 does not need to be crashed).
By varying the number of weeks by which we crash the project we can construct the graph shown below. In that graph we have plotted, for each possible project completion time, the minimum cost associated with achieving that completion time.
Note here that this graph contains three distinct straight line segments (16 to 18, 18 to 21, 21 to 24). In general it is always true that the cost/time tradeoff graph contains a number of distinct straight line segments (i.e. mathematically we would say that it is piecewise linear). This arises because of the linear relationship that was assumed to hold between cost and completion time for each activity.
Note there that the package merely provides information, in this case the cost of the project for all possible completion times between 16 and 24 weeks. It does not tell you which completion time you should choose (as you can have any completion time between 16 and 24 weeks provided you are prepared to pay for it!). What the package does is enable you, as the project manager, to make an informed choice about the completion time to have.
For the network considered above we have seen that the minimum possible completion time (associated with the maximum cost) is 16 weeks. But what if we really wanted a completion time of 15 weeks - is there any possible way of achieving that?
The simple answer is NO, but with a caveat, not with the project as currently represented by the network. It may be that we can change our project network, opening up the possibility of (potentially) reducing the overall project completion time below 16 weeks. A common approach to do this is activity splitting.
In activity splitting we (typically) examine each critical activity (since critical activities are the determining factor in overall project completion) and see if they can be split into two (or more) separate activities. For example, for the network considered before we might decide that activity 1, requiring 6 weeks can be split as below:
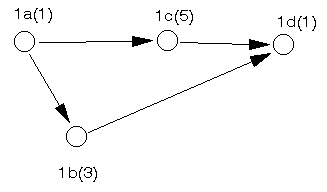
Here we have split this activity into 4 sub-activities 1a,1b,1c,1d (and their precedence relationships). It can be seen that by so doing we have actually increased the time required to complete activity 1 to 7 weeks, from the original 6 weeks. However, it may be that this subdivision of activity 1, when considered from the cost crashing point of view, gives us more flexibility.
For example before subdivision we could only crash activity 1 down from 6 weeks to 4 weeks. If we could now crash activity 1b by 2 weeks and activity 1c by 3 weeks then we could crash activity 1 down from 7 weeks to 3 weeks - hence potentially reducing the overall project duration below the 16 week barrier we previously encountered.
Obviously the practicality of subdividing, and then crashing, critical activities depends upon the context but the above example does illustrate that sometimes close examination of critical activities with a view to subdivision can pay benefits.
Because cost crashing can be modelled and solved via linear programming we have a number of alternative options available, as the package illustrates. For example we might be interested in finding the minimum time in which we can complete the project subject to a constraint (limitation) upon the total cost. This is illustrated below using the package for a total cost of 550.
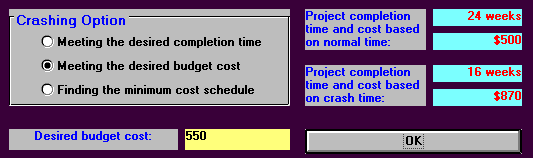
It can be seen above that the minimum completion time subject to a cost constraint of 550 is 21.5 weeks.
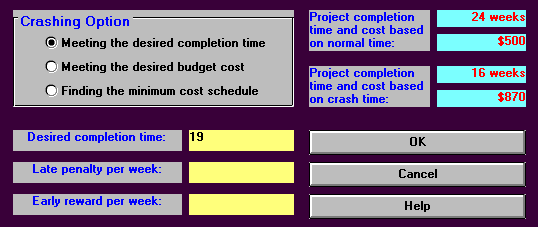
The package also allows us to balance rewards in meeting a target desired project completion time as against penalties for missing this completion time. The example below illustrates this where the desired project completion time is 20 weeks, each week we are late (complete after week 20) costs us 50 and each week we are early (complete before week 20) earns us a reward of 75.

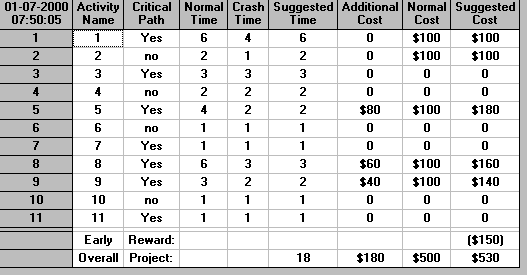
It can be seen that the optimum (least cost) completion time in this situation is 18 weeks, leading to a total minimum cost of 530.
PERT/Cost is a way of showing the budgeted project cost based on the activity start times. The assumption behind PERT/Cost is that cost per unit of time for an activity is constant between its start time and its finish time. For example, let us return to the original network we had before with the original crashing data as illustrated below.

Deciding to complete the project in 18 weeks gives the output below.
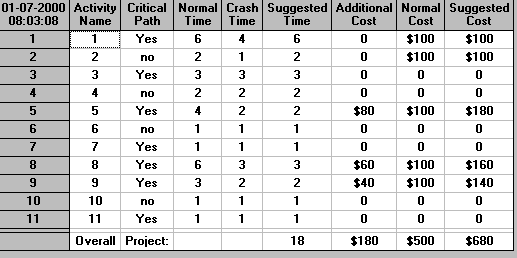
The basic assumption in PERT/Cost is that the cost of an activity is spread uniformly over its duration. So, for example, activity 1, with a suggested time of 6 costs us 100, i.e. 100/6 = 16.67 for each week during which activity 1 is done. Activity 2, with a suggested time of 2 costs us 100, i.e. 100/2 = 50 for each week during which activity 2 is done.
We have stressed above the weeks during which an activity is done. Whilst any activities which are critical must be performed at precise times in order to complete the overall project in 18 weeks is the same true of non-critical activities?
For this project with a completion time of 18 weeks the Activity Criticality Analysis is

Activity 2, for example (which requires 2 weeks) is non-critical and has a slack of 6 weeks. It can potentially be started at any time between week 0 (its earliest start time) and week 6 (its latest start time) without affecting the overall project completion time. If we were to start it in week 4, for example, the cost of 50 per week associated with activity 2 would not be incurred until week 4. This may potentially be of benefit (why incur a cost before you need to?).
In PERT/Cost we can produce a graphic (as below) showing the cost of the project
This is shown below for the project considered above completing in 18 weeks. In that figure the ES line is shown in purple, and the LS line in blue.
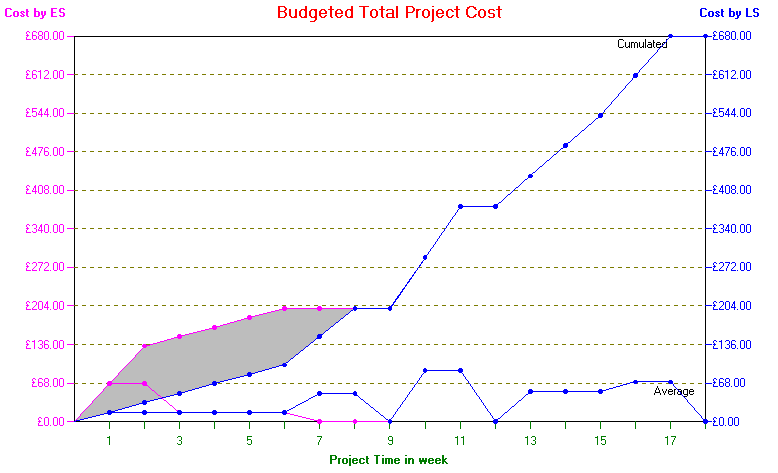
The gap between the cumulative ES and LS lines represents flexibility - cost can be adjusted within the ES and LS limits by artificially delaying the start of non-critical activities.
It is important to note however that artificially delaying the start of non-critical activities (and hence incurring activity costs later) is not free. Rather it costs us. Simply put time lost by delaying the start of an activity cannot later be regained (if things do not turn out as planned) given the desired fixed completion time for the overall project.
The package contains two facilities for monitoring the progress of the project, one with respect to time and the other with respect to cost. To illustrate these we have expanded the input as below to include the actual cost incurred so far on each activity and the percentage by which it has completed.
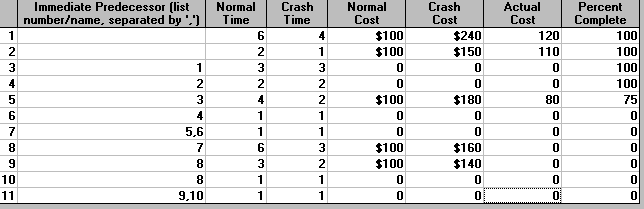
Supposing that we are using just normal times (and costs) and that it is currently week 10. Then we can get an indication of the time progress of the project by Solve Critical Path Using Normal Times and then using Project Completion Analysis to get the output below.
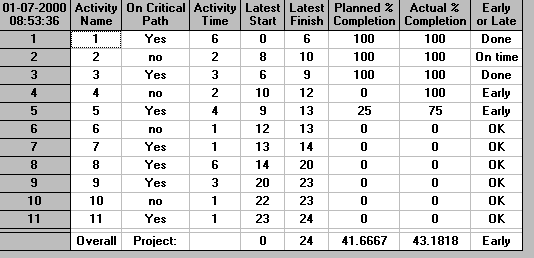
Using Project Cost Control we can get an indication of the cost progress of the project at the same time as below.
Recall that previously we formulated our network problem as a linear program. To remind you of it we briefly repeat this formulation below.
Below we repeat the network diagram for the problem we considered before. However note that we have now added a dummy activity (12) with a completion time of zero to represent the end of the project. This just makes the calculations we have to do easier to follow.
In order to analyse this network by linear programming let xi (>=0) represent the time at which we start activity i. Then the linear programming formulation of the above network problem is
minimise x12
subject to
x3 >= x1 + 6
x4 >= x2 + 2
x5 >= x3 + 3
x6 >= x4 + 2
x7 >= x5 + 4
x7 >= x6 + 1
x8 >= x7 + 1
x9 >= x8 + 6
x10 >= x8 + 6
x11 >= x9 + 3
x11 >= x10 + 1
x12 >= x11 + 1
xi >=0 i=1,2,...,12
and note here that the activity completion times used here correspond to the normal times for our cost crashing example.
Now to expand this formulation to include cost crashing let ci be the number of time units (weeks in this case) by which we choose to crash (reduce) the completion time of activity i. Recalling the problem (as below)

we have that only activities 1,2,5,8,9 can be crashed in this example so we need only define crash variables for those activities. These crash variables must satisfy
0 <= c1 <= 2 (activity 1 can be crashed by at most
2 time units)
0 <= c2 <= 1 (activity 2 can be crashed by at most 1 time
units)
0 <= c5 <= 2 (activity 5 can be crashed by at most 2 time
units)
0 <= c8 <= 3 (activity 8 can be crashed by at most 3 time
units)
0 <= c9 <= 1 (activity 9 can be crashed by at most 1 time
units)
The key to amending the formulation is to note that wherever a completion time for an activity appears in the formulation above it must be changed to completion time - crash variable. Hence the first constraint x3 >= x1 + 6 which says that the start time for activity 3 must be at least as big as the start time for activity 1 plus 6 (the completion time for activity 1) is now changed to x3 >= x1 + 6 - c1, since the completion time for activity 1 has effectively changed to 6-c1. Note that the cost associated with c1 is 70c1, since each week that we crash activity 1 costs us 70.
Continuing in this vein the complete LP formulation of the problem of determining the minimum cost way of crashing the project to achieve a given completion time T is given by
minimise 70c1 + 50c2 + 40c5 + 20c8 + 40c9
subject to
x12 = T
x3 >= x1 + 6 - c1
x4 >= x2 + 2 - c2
x5 >= x3 + 3
x6 >= x4 + 2
x7 >= x5 + 4 - c5
x7 >= x6 + 1
x8 >= x7 + 1
x9 >= x8 + 6 - c8
x10 >= x8 + 6 - c8
x11 >= x9 + 3 - c9
x11 >= x10 + 1
x12 >= x11 + 1
0 <= c1 <= 2
0 <= c2 <= 1
0 <= c5 <= 2
0 <= c8 <= 3
0 <= c9 <= 1
xi >= 0 i=1,2,...,12
To ease the notation below we will refer to all the constraints above (excluding the single constraint x12 = T) as the constraint set CS.
This linear program (LP) can be solved using the package as below, for T=19. The input (in part) needed to enter the LP is:


with the solution being
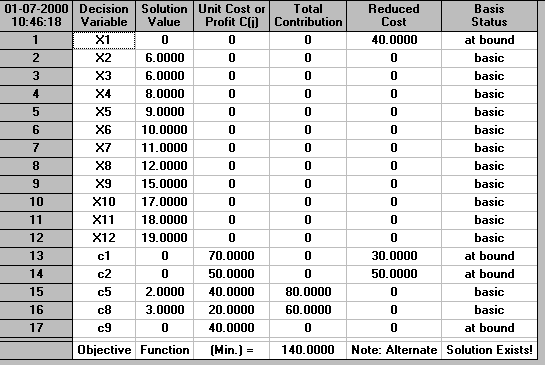
This has the same additional cost of 140 as before, but has a different structure. Here we have decided to crash activity 5 by two weeks and activity 8 by three weeks. In the results from the package for crashing 19 weeks before we crashed activity 5 by one week, activity 8 by three weeks and activity 9 by one week.
In fact this original structural solution can be found by using Obtain Alternative Optimal to get
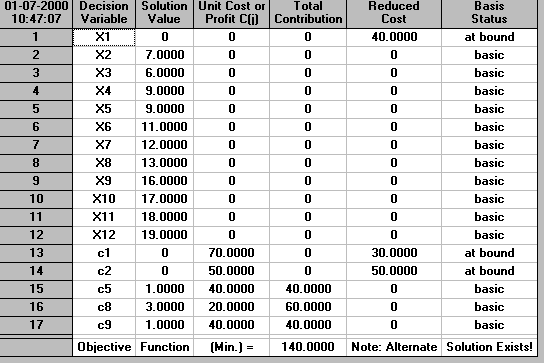
The package also had the facility to find the minimum project completion time satisfying a cost constraint. To achieve this we simply need the LP
minimise x12
subject to the constraint set CS we had before and
70c1 + 50c2 + 40c5 + 20c8 + 40c9 <= cost limit
The package also had the facility to find the best project completion time when there were penalties for late completion and rewards for early completion. To formulate this let the desired completion time be D, the penalty for late completion be P per time unit (week in this case) late, the reward for early completion be R per time unit (week in this case) early. Note that all these are known numbers, not variables.
Then to find the best project completion time the ONLY APPROPRIATE APPROACH is to solve two LPs. One assuming we finish "early" and the other assuming we finish "late". Comparing the cost of the optimal solutions to these LPs will give us the best project completion time.
This solution of two LPs as being the only appropriate approach is stressed above. This is because it is commonly believed that the problem of finding the best project completion time when there were penalties for late completion and rewards for early completion can be correctly solved using just a single LP. Indeed this is the approach used by the package. However this is simply incorrect, as the example below illustrates.
More formally the LP associated with assuming that we finish "early" is
minimise 70c1 + 50c2 + 40c5 + 20c8
+ 40c9 - R*(D - x12)
subject to the constraint set CS we had before and
x12 <= D (finish at or before the desired completion time)
Similarly the LP associated with assuming that we finish "late" is
minimise 70c1 + 50c2 + 40c5 + 20c8
+ 40c9 + P*(x12 - D)
subject to the constraint set CS we had before and
x12 >= D (finish at or after the desired completion time)
With D=20, R=75 and P=50, which was the case dealt with by the package before above, the LP for finishing early can be solved as below to give a solution with x12=16 and cost 20 (after adjusting the cost of the LP for the constant term -R*D = -75*20 = -1500 in this case)


The LP for finishing late can be solved as below to give a solution with x12=20 and cost 100 (after adjusting the cost of the LP for the constant term -P*D = -50*20 = -1000 in this case)

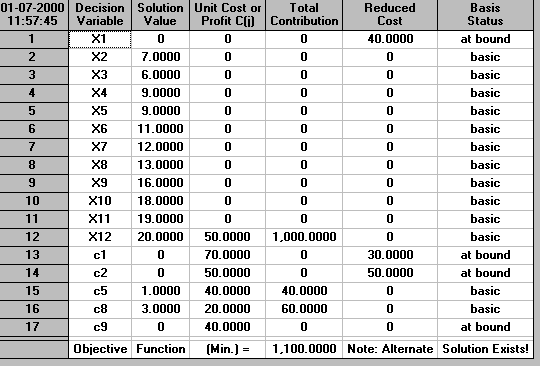
Hence using our two LP approach it is clear that:
Hence overall the best solution is to crash the project to complete in 16 weeks, at a total crashing cost (after rewards for early completion) of 20. Note that in computing this cost figure of 20 we have not accounted for the total ordinary Normal Cost (since that must be incurred anyway) and so adding this in (total cost 500) we have that this solution is of value 520.
Compare now the solution obtained by the package, which was of total cost 530 associated with a completion time of 18 weeks. This was obtained using the (incorrect) single LP approach.
In fact we could have detected that the package solution was in error before now. We actually crashed the project to 16 weeks and had an associated cost of 820. Now finishing in 16 weeks incurs a reward of 4*75 = 300 giving a total cost of 820 - 300 = 520. The same cost as given by our correct two LP approach but contradicting the cost of 530 given by the package using the single LP approach.