OR-Notes are a series of introductory notes on topics that fall under the broad heading of the field of operations research (OR). They were originally used by me in an introductory OR course I give at Imperial College. They are now available for use by any students and teachers interested in OR subject to the following conditions.
A full list of the topics available in OR-Notes can be found here.
We follow the same approach as we used for formulating IP's - namely:
Here we are trying to decide whether to undertake a project or not (a "go/no-go" decision).
To define the variables we use the verbal description of
xj = 1 if we decide to do project j (j=1,...,4) = 0 otherwise, i.e. not do project j (j=1,...,4)
Note here that, by definition, the xj are integer variables which must take one of two possible values (zero or one).
The initial constraints relating to the availability of capital funds each year are:
0.5x1 + 1.5x3 + 0.1x4 <= 3.1 (year
1)
0.3x1 + 0.8x2 + 1.5x3 + 0.4x4
<= 2.5 (year 2)
0.2x1 + 0.2x2 + 0.3x3 <= 0.4 (year
3)
To ensure that projects 1 and 2 are mutually exclusive we have the constraint:
x1 + x2 <= 1
To add the return from project 4 (if chosen) to the capital available in year 3 we amend the year 3 constraint:
0.2x1 + 0.2x2 + 0.3x3 <= 0.4
to
0.2x1 + 0.2x2 + 0.3x3 <= 0.4 + 0.1x4
To maximise the total return - hence we have
maximise 0.2x1 + 0.3x2 + 0.5x3
and note here how project 4 does not contribute to the objective.
This gives us the complete IP which we write as
maximise 0.2x1 + 0.3x2 + 0.5x3
subject to
0.5x1 + 1.5x3 + 0.1x4 <= 3.1
0.3x1 + 0.8x2 + 1.5x3 + 0.4x4
<= 2.5
0.2x1 + 0.2x2 + 0.3x3 - 0.1x4
<= 0.4
x1 + x2 <= 1
xj = 0 or 1 j=1,...,4
Solution - using Solver
Below we solve the problem with the Solver add-in that comes with Microsoft Excel.
If you click here you will be able to download an Excel spreadsheet called ip_class9.xls that already has the IP we are considering set up.
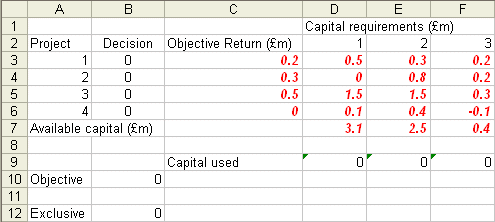
Take this spreadsheet and look at Sheet A. You should see the problem we considered above set out as:

Here we have set up the problem with the decisions (the zero-one variables) being shown in cells B3 to B6. The capital used in each of the three years is shown in cells D9 to F9 and the objective (total return) is shown in cell B10 (for those of you interested in Excel we have used SUMPRODUCT in cells D9 to F9 and B10 as a convenient way of computing the sum of the product of two sets of cells).
Note the -0.1 in cell F6 as a convenient way of representing the addition to capital in year 3 if we choose to do project 4.
Cell B12 holds the sum of B3 and B4, concerned with the two projects that are mutually exclusive.
Doing Tools and then Solver you will see:
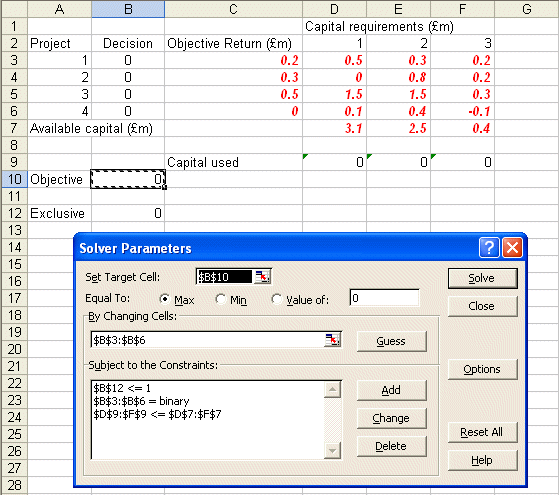
where B10 is to be maximised (ignore the use of $ signs here - that is a technical Excel issue if you want to go into it in greater detail) by changing the decision cells B3 to B6 subject to the constraints that these cells have to be binary (zero-one) and that D9 to F9 are less than or equal to D7 to F7, the capital availability constraints. B12 deals with the constraint that projects 1 and 2 are mutually exclusive.
Clicking on Options on the above Solver Parameters box you will see:

showing that we have ticked Assume Linear Model and Assume Non-Negative.
Solving we get:
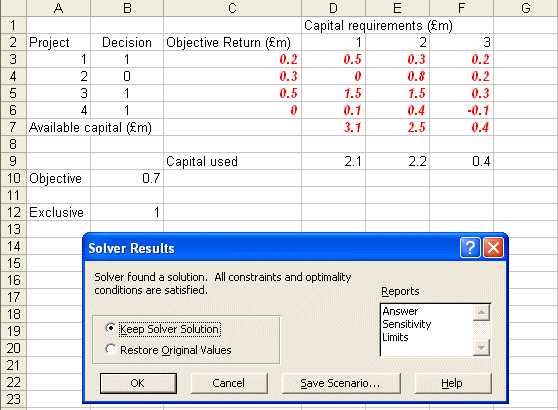
indicating that the optimal decision (the decision that achieves the maximum return of 0.7 shown in cell B10) is to do projects 1, 3 and 4 (the decision variables are one in cells B3, B5 and B6, but not to do project 2 (the decision variable is zero in cell B4).