OR-Notes

J E Beasley

OR-Notes are a series of introductory notes on topics that fall under the broad heading of the field of operations research (OR). They were originally used by me in an introductory OR course I give at Imperial College. They are now available for use by any students and teachers interested in OR subject to the following conditions.

A full list of the topics available in OR-Notes can be found here.

Network analysis - cost/time tradeoff tutorial solution

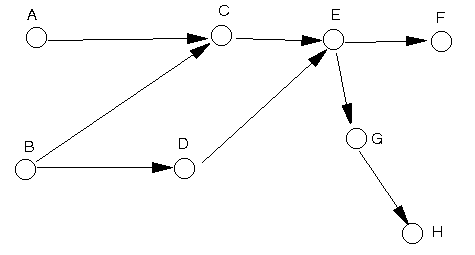
The network diagram is shown below.

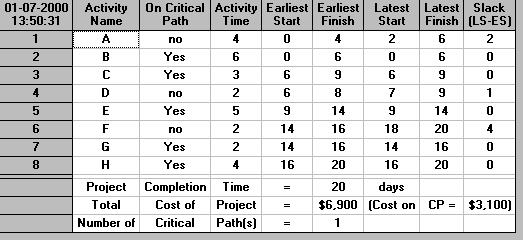
Using the package the project duration using normal times is 20 days and the critical path B-C-E-G-H, as below.

To crash the project by one day list all the crashable activities on the critical path and their associated incremental cost:

• B incremental cost 400
• C incremental cost 200
• E incremental cost 250
• G incremental cost 300
• H incremental cost 400

The lowest incremental cost is associated with activityC and hence we choose to crash activity C by one day. The new situation after activity C has been crashed is shown below.

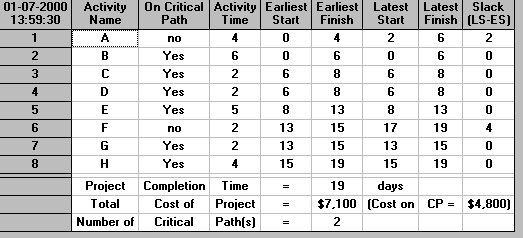
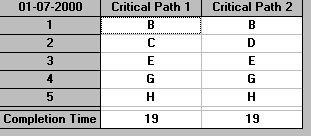
Note that we now have two critical paths - which complicates things.

Again we list all the crashable activities on the critical paths and their associated incremental cost:

• B incremental cost 400
• D incremental cost 500
• E incremental cost 250
• G incremental cost 300
• H incremental cost 400

Note that C, although on a critical path, is not listed here. This is because it has already been crashed to its maximum extent.

Examining the critical paths of B-C-E-G-H and B-D-E-G-H it is clear that:

• crashing B, E, G or H would reduce the duration of each critical path and so would reduce the completion time of the entire project;
• crashing D would achieve nothing since the other critical path B-C-E-G-H would still dominate (and C cannot be crashed).

From B, E, G or H the best choice is E with an incremental cost of 250 and so we would choose to crash E by one day.

In order to formulate the problem consider the same network diagram as above, but with a dummy end activity (I) added as below.

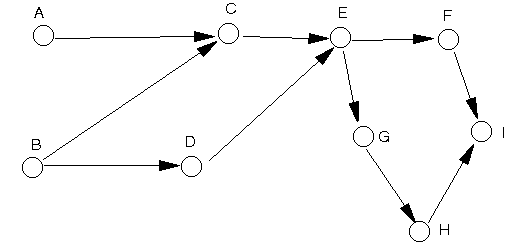
Using a similar notation as in the lecture notes let x_A, x_B, etc be the starting times for each activity and c_A, c_B, etc be the number of days by which we reduce (crash) each activity. Taking each precedence relationship in the above network in turn and making use of the normal times we have the constraints:

x_C >= x_A + 4 - c_A
x_C >= x_B + 6 - c_B
x_D >= x_B + 6 - c_B
x_E >= x_C + 3 - c_C
x_E >= x_D + 2 - c_D
x_F >= x_E + 5 - c_E
x_G >= x_E + 5 - c_E
x_H >= x_G + 2 - c_G
x_I >= x_H + 4 - c_H
x_I >= x_F + 2 - c_F

all x variables >=0

The constraints limiting the crashing for each activity are:

0 < = c_A <= 1
0 < = c_B <= 3
0 < = c_C <= 1
0 < = c_D <= 1
0 < = c_E <= 2
0 < = c_F <= 1
0 <= c_G <= 1
0 <= c_H <= 2

Introducing a variable d >= 0 to "represent" the number of days we finish past day 14 we have

d >= x_I - 14

our objective is:

minimise 250x_I + 100d + 100c_A + 400c_B + 200c_C +500c_D + 250c_E + 100c_F + 300c_G + 400c_H

and this completes our LP formulation.

If activity B can be crashed by a further day, at an additional cost of 750, then introduce an additional variable c_BB indicating whether we crash B by this additional day or not, where 0 <= c_BB <=1 and:

• add 750c_BB to the objective given above
• modify the constraints involving the completion time of B as:
• x_C >= x_B + 6 - c_B becomes x_C >= x_B + 6 - c_B - c_BB
• x_D >= x_B + 6 - c_B becomes x_D >= x_B + 6 - c_B - c_BB