OR-Notes are a series of introductory notes on topics that fall under the broad heading of the field of operations research (OR). They were originally used by me in an introductory OR course I give at Imperial College. They are now available for use by any students and teachers interested in OR subject to the following conditions.
A full list of the topics available in OR-Notes can be found here.
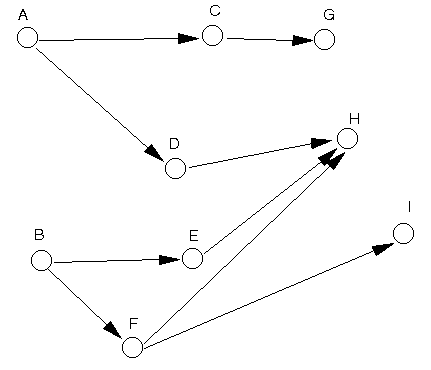
The network diagram is shown below.

Utilising the package the solution is

so the expected completion time is 16 months. In order to calculate the probability of completing the project in 18 months we can use the package and get

so a probability of 87.373%.
Performing the probability calculation manually the critical path is B-E-H so (using the notation in the notes) T=18, C=16 and V= (0.3333)2 + (1.5)2 + (0.8333)2 =3.0555
Hence z=(T-C)/V0.5 = (18-16)/(3.0555)0.5 = 1.14 (to two decimal places). Utilising the tables in the notes the probability of observing a value from the standard normal distribution N(0,1) with value z or less is 0.873. Hence the probability of completing the project within 18 months is 87.3% which agrees well with the figure calculated above.
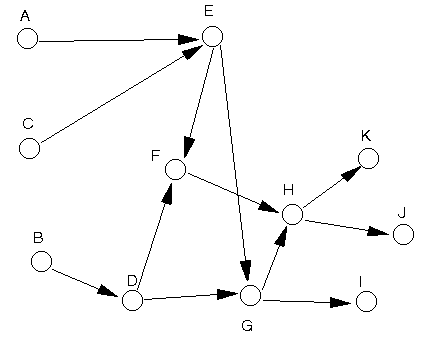
The network diagram is shown below.
Utilising the package the solution is
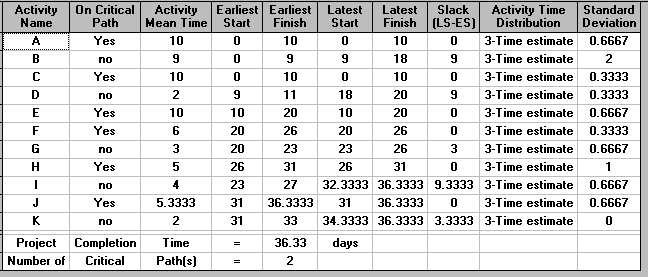
so the expected completion time is 36.33 days. Note here that there are two critical paths in this example, namely
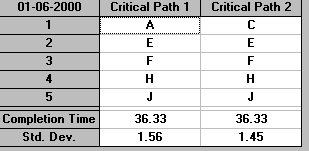
In order to calculate the probability of completing the project in 38 days we can use the package and get

and it can be clearly seen that the package gives a nonsense answer! This shows that software cannot be trusted!
Performing the probability calculation manually the first critical path is A-E-F-H-J so (using the notation in the notes) T=38, C=36.33 and V= (0.6667)2 + (0.6667)2 + (0.3333)2 + (1)2 + (0.6667)2 = 2.4446
Hence z=(T-C)/V0.5 = (38-36.33)/(2.4446)0.5 = 1.07 (to two decimal places). Utilising the tables in the notes the probability of observing a value from the standard normal distribution N(0,1) with value z or less is 0.858.
For the second critical path of C-E-F-H-J we have that T=38, C=36.33 and V= (0.3333)2 + (0.6667)2 + (0.3333)2 + (1)2 + (0.6667)2 = 2.1112
Hence z=(T-C)/V0.5 = (38-36.33)/(2.1112)0.5 = 1.15 (to two decimal places). Utilising the tables in the notes the probability of observing a value from the standard normal distribution N(0,1) with value z or less is 0.875.
Multiplying the two probabilities together we have that the calculated probability of completing the project within 38 days is (0.858)(0.875) = 0.751
Hence the probability of taking longer than 38 days is 1-0.751 = 0.249 = 24.9%
Note here however that, plainly, the two critical paths are not independent and so this throws this probability calculation into doubt. Utilising the package and performing a simulation we get the results below

Hence, after simulating for a reasonable time period, we find a probability of completing the project within 38 days of 82.26%. This shows that, for this particular example, the probability estimate of 75.1% obtained above is substantially in error.