
OR-Notes are a series of introductory notes on topics that fall under the broad heading of the field of operations research (OR). They were originally used by me in an introductory OR course I give at Imperial College. They are now available for use by any students and teachers interested in OR subject to the following conditions.
A full list of the topics available in OR-Notes can be found here.
To incorporate the condition that either the company makes none of variant 2 or it makes at least 18,000 units we have that, in terms of the variables we have already defined above, this condition is "either x2 = 0 or x2 >= 18,000". The standard trick for dealing with "either/or" conditions relating to a single variable is to introduce a zero-one variable (y, say) defined by the verbal description
y = 1 if we produce variant 2 and hence x2 >= 18,000 = 0 otherwise (i.e. x2 = 0)
To turn this verbal description into an equivalent mathematical description the trick is to add the two constraints
x2 <= My (1) and x2 >= 18000y (2)
to the formulation of the problem where M is a positive constant and represents the most of variant 2 that we could possibly make (e.g. for this example a suitable value for M (deduced from the operation time limits) would be M=min[100,000/4; 50,000/2; 60,000/3] = 20,000).
To verify that these two equations are equivalent to our verbal description of the problem we tabulate, for each possible value of y, the meaning of the corresponding mathematical and verbal descriptions as below.
Variable value Mathematical description Verbal description
y = 0 (1) x2 <= 0 x2 = 0
(2) x2 >= 0
i.e. x2 = 0
y = 1 (1) x2 <= 20,000 x2 >= 18,000
(2) x2 >= 18,000
which since x2 must
always be <= 20,000
from other constraints
means x2 >=18,000
It is clear from this tabulation that the mathematical and verbal descriptions are equivalent.
To incorporate the condition relating to fixed cost we have the standard trick of introducing a zero-one variable (z, say) defined by the verbal description
z = 1 if we incur the fixed cost (i.e. x4 >= 0) = 0 otherwise (i.e. no fixed cost incurred so x4 = 0)
To turn this verbal description into a mathematical description the trick is to
(1) add a term -250z to the objective function; and (2) add the constraint x4 <= Nz
where N is a positive constant and represents the most of variant 4 that we could possibly make (e.g. for this example a suitable value for N (deduced from the operation time limits) would be N=min[100,000/7; 50,000/4; 60,000/5] = 12,000).
To show that these two equations are equivalent to our verbal description of z we tabulate, for each possible value of z, the meaning of the corresponding mathematical and verbal descriptions as below.
Variable value Mathematical description Verbal description
z = 0 (1) objective function +0 no fixed cost incurred
(2) x4 <= 0 i.e. x4 = 0 x4 = 0
z = 1 (1) objective function -250 fixed cost incurred
(2) x4 <= 12,000 x4 >= 0
It is clear that for the case z = 0 the mathematical and verbal descriptions are identical.
For the case z = 1 these descriptions could be different if we had x4 = 0 (satisfying x4 <= 12,000). However this cannot occur at the optimal solution because if it did we could change the value of z from one to zero without violating x4 <= 12000z (remember x4 = 0) thereby decreasing the value of the objective function (by 250) and violating the optimality assumption (since at the optimal solution it is impossible to improve (decrease in this example) the value of the objective function). Hence the mathematical and verbal descriptions are identical.
The complete formulation of the problem is therefore:
maximise 1.5x1 + 2.5x2 + 3.0x3 + 4.5x4 - 250z subject to x2 <= 20000y x2 >= 18000y x4 <= 12000z plus the constraints involving Tass, Tpol, Tpac given before xj >= 0 j=1,...,4 y = 0 or 1 z = 0 or 1
Note that (strictly) in this formulation some variables can take only integer values (y, z) and some variables can take fractional values (xj j=1,2,3,4). This formulation is therefore an example of a mixed-integer program (MIP).
The input to the package for this problem is shown below, as is the solution output.

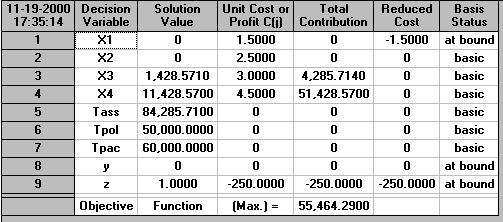
You can see from this output that the optimal solution is to produce just variants 3 and 4. As commented above y and z are integers, whereas x3 and x4 are fractional. However as the number of units produced is large rounding these fractional values to the nearest integer is acceptable in practice (remember some of the numbers used in the formulation will not be completely accurate).