
Une technique déclarative pour filtrer des
motifs topologiques de protéines
David Gilbert*,*** — David Westhead**,*** —
Janet Thornton***,****,***** — Karine Yvon*
*
drg@cs.city.ac.uk : Department of Computer Science, City University, London EC1V OHB, UK**
Current address: School of Biochemistry and Molecular Biology, University of Leeds, Leeds LS2 9JT,UK***
European Institute of Bioinformatics, Hinxton, Cambridge CB10 1SD, UK****
Departement of Biochemistry, University College, London WC1E 6BT, UK*****
Crystallography Dept., Birkbeck College, London WC1E 7HX, UK
RESUME
. Nous décrivons ici une méthode permettant un filtrage rapide de motifs à partir de descriptions topologiques de structures de protéines. Cette méthode a été implémentée en programmation logique par contraintes sur des domaines finis, et forme la base d’une technique de filtrage de structures de protéines [GWVT00]. Le système est accessible sur le site web de l’Institut Européen de Bio-informatique (http://tops.ebi.ac.uk/tops).
ABSTRACT. We describe a constraint-based method to perform fast matching of motifs with topological descriptions of protein structures. This method has been implemented using finite domain logic programming, and forms the basis of a protein structure comparison technique which we have described elsewhere [GWVT00]. The system is accessible at the web-site of the European Bioinformatics Institute (
http://tops.ebi.ac.uk/tops)MOTS-CLES. Topologie de protéines, motifs, filtrage de formes, contraintes.
KEYWORDS. Protein topology, motifs, pattern matching, constraints.
HERMES Science publications
L’étude des structures atomiques tri-dimensionnelles ou du repliement des molécules de protéines globulaires a toujours été un aspect très important de la biologie moléculaire depuis la détermination expérimentale des premières structures, il y a plus de 30 ans. Ces molécules sont responsables de l’exécution et de la régulation de la plupart des processus essentiels à la vie. Pour ne mentionner que quelques uns de ces processus: les protéines de type enzyme catalysent d’importantes réactions biochimiques, les facteurs de transcription régulent l’utilisation de l’ADN par la cellule, les anticorps du sytème immunitaire reconnaissent les molécules étrangères, etc. La connaissance de ces structures de protéines a permis aux biologistes de, premièrement, mieux comprendre la fonction d’une protéine et comment cette fonction est accomplie, et, deuxièmement, de comprendre en détail les relations évolutives entre les différentes protéines.
Une protéine est composée d’une chaîne ou séquence d’acides aminés. Vingt différents types d’acides aminés sont produit naturellement. Dans les protéines globulaires, cette chaîne d’acides aminés se replie sur elle-même produisant une forme globulaire (la structure ou repliement). Certaines chaînes se replient en 2 unités globulaires compactes ou davantage. Ces unités sont appelées domaines et sont souvent associées aux différentes activités partielles de la protéine. Les sections de la chaîne protéinique, composées d'hélices-α
La figure 1 ci-dessous illustre bien ce modèle de structure: exemple de la chaîne A de la protéine 2bop [HGLS92]. Noter que les ESS de type étendu (brin) sont représentés par des rubans gris clairs, les hélices par des rubans gris foncés et les boucles les reliant, par de minces cordons. La structure est à tri-dimensionnelle. Pour bien se rendre compte, il faudrait visualiser cette structure sur écran en utilisant un programme comme Rasmol [SMW95], celui-ci permettant d'observer un objet sous différents angles de rotation.

Figure 1. diagramme rasmol de la protéine 2bop
Actuellement, les structures de protéines sont déterminées de façon expérimentale par la radiocristallographie et la RMN (Résonance Magnétique Nucléaire), deux techniques très longue à effectuer. Lorsque les coordonnées atomiques sont déterminées, les biologistes cherchent à établir le lien entre la protéine sous étude et d’autres protéines dont les structures et fonctions ont déjà été identifiées. Une parfaite compréhension des similarités et des différences entre les structures de protéines est essentielle à l’étude des relations entre séquences, structures et fonctions, et à l’analyse des relations possibles d’évolution. Ceci est à l'origine du développement de méthodes computationnelles de comparaison de structures et d’algorithmes de recherche de bases de données structurelles telle que la banque de données Brookhaven Protein Data Bank (PDB) [BKW+77, ABB+87]. Ce domaine de recherche est beaucoup trop vaste pour rapporter ici son contenu, le lecteur est invité a consulté Orengo [Ore94] et Gibrat et al [GMB96] pour une excellente étude du sujet.
Les structures de protéines peuvent être représentées à différents niveaux de détails, allant de la description des coordonnées atomiques, en passant par l’approximation des vecteurs, aux ESS, et ce en terminant par des méthodes de description basées sur des modèles de structures hautement simplifiés. Ces méthodes de description, plus précisément de description topologique, considèrent une séquence d' ESS, en prenant compte de certaines relations comme la juxtaposition spatiale au sein du repliement et l'orientation approximative, et en négligeant certains détails comme la longueur et la structure des boucles et la longueur des éléments de structure secondaire.
La description topologique a l’avantage d’être simple, ce qui rend possible l’implémentation d’algorithmes très rapides de recherche de motifs et de comparaison de structures. Ces descriptions peuvent également être utilisées dans des applications comme l’apprentissage automatique. Sans elles, il serait bien difficile d'appliquer de telles applications aux structures de protéines. Négliger certains détails qui généralement varient entre structures apparentées, par exemple la longueur et la structure des boucles, la longueur exacte des ESS, la position spatiale et l’orientation des SSE, offre la possibilité de détecter des relations structurales beaucoup plus distantes, plus que ne permettaient les méthodes traditionnelles de description geométriques. Mais d’un autre côté, quelques inconvénients peuvent faire surface: des exemples de structures, qui, certes, sont apparentés au niveau topologique, sont détectés alors qu’ils sont en fait très différents d’un point de vue géométrique et n’ont aucune relation biologique significative.
Dans cet article, nous présentons de façon formelle les descriptions topologiques de structures et motifs de protéines. Nous présentons également un algorithme rapide de retour-arrière, fonctionnant à partir de contraintes, qui filtre un motif dans une description de structure donnée. Nous décrivons l'implémentation des descriptions topologiques en base de données déclarative et l'algorithme de filtrage en un programme logique par contraintes sur domaines finis. Nous incluons dans ce document quelques résultats illustrant l'utilité de notre programme dans sa recherche de motifs dans une base de données de protéines.
Les structures de protéines sont représentées dans notre système sous forme topologique, utilisant le modèle TOPS qui est une abstraction schématique en 2 dimensions de structures de protéines tri-dimensionnelles. Créé à l’origine pour une comparaison manuelle et pour la compréhension des repliements de protéines, les croquis TOPS étaient dessinés à la main [ST77]. Il existe maintenant un algorithme informatisé qui produit ces croquis automatiquement à partir d'une structure de protéine [FMT94,WSFT99,WHT98]. Nous avons basé cette technique sur la version formelle du langage TOPS que nous avons conçu. Celle-ci contient des contraintes sur domaines finis, et utilise aussi bien les diagrammes (descriptions des exemples) que les caractérisations plus générales des structures de protéines (motifs).
Un diagramme TOPS est une formalisation d’un croquis, basé sur les informations topologiques sous-jacentes des ESS (liaisons hydrogènes et chiralités) à partir desquelles le croquis est généré. Un tel diagramme est une séquence de structure secondaire et deux ensembles correspondants qui définissent les relations, ou contraintes, des éléments de la séquence. Ces relations sont sous forme de liaisons hydrogènes ou de chiralités.
De façon plus formelle, un diagramme TOPS est un triplet T = (E,H,C) où E = S1,…,Sk est une séquence d’éléments de structure secondaire de longueur k et H et C sont des relations sur SSE, appelés respectivement liaisons hydrogènes et chiralités. Dans cette description, une contrainte de liaison hydrogène fait référence à une échelle de liaisons hydrogènes individuelles entre brins adjacents du feuillet. Nous caractérisons un diagramme TOPS tel un graphe-chaîne, car une séquence E peut être considérée comme une chaîne, avec 2 relations H et C sur les éléments de la chaîne, ou comme une trajectoire le long du graphe ayant pour sommets {S1, …, Sk} et pour flèches {S1 → S2, S2 → S3, …, SK-1 → SK}, et 2 ensembles H et C d’arêtes sur un sous-ensemble des sommets. C'est pourquoi nous utilisons indiffèremment, ci-dessous, les termes 'longueur du diagramme' et 'longueur de la séquence E'.
Dans notre formalisme, un SSE est
Les liaisons hydrogènes et chiralités sont toutes deux des relations symétriques (les arêtes du graphe). Les deux ESS contenus dans une liaison hydrogène doivent obligatoirement être des brins. A chaque liaison est associée une direction relative d Î {P, A}, indiquant si la liaison s’est accomplie entre brins parallèles ou anti-parallèles. A chaque chiralité est associée une variété optique, variété ne pouvant être que l'inverse l'une de l'autre,
χ Î {G,D} (respectivement gauche et droite). Une chiralité ne se forme qu'entre pair d'ESS de même type. La relation de liaison hydrogène entre deux ESS Si et Sj est dénotée par (Si, d , Sj) et celle de chiralité par (Si, χ, Sj).La définition formelle d’un diagramme TOPS est la suivante:
Diagramme = (S,Hd, Cd), soit S = {a +, a -, b +, b -} où
S = (S1,..., Sk), 1£ i£ k, Si Î S
Hd = {(Si,d ,Sj), | Si,Sj, Î {b +, b -} d = P ↔ Si=Sj, d = A ↔ Si¹ Sj}
Cd = {(S1, χ,Sj) | Si,Sj, Î S , , χ Î {G,D}
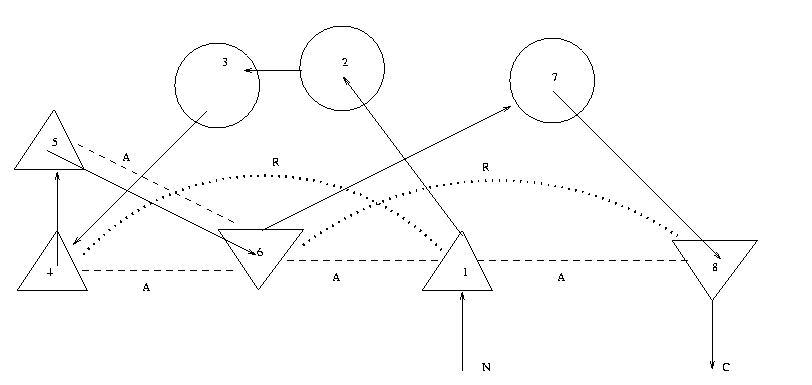
Exemple: considérons le diagramme TOPS représentant la protéine 2bop (figure 2). Le diagramme peut être en quelque sorte 'allongé' de façon linéaire, voir figure 3. La protéine est ainsi définie :
2bop = (S,H,C) où
S=(b 1+, a 2-, a 3-, b 4+, b 5+,b 6-, a 7+, b 8-)
H = { (b 1+, A, b 6-), (b 1+, A, b 8-), (b 4+, A, b 6-),(b 5+, A, b 6-)}
 C= {(b
1+,R, b
4+),(b
6-,R, b
8-)}
C= {(b
1+,R, b
4+),(b
6-,R, b
8-)}
Figure 2. Diagramme TOPS de la protéine 2bop
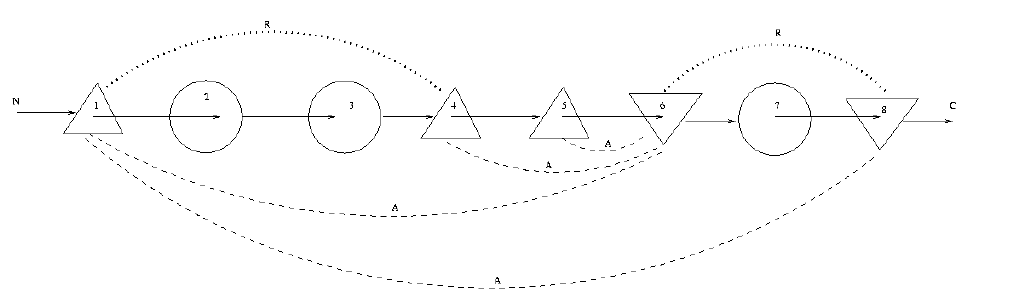
Figure 3. Diagramme linéaire TOPS de la protéine 2bop
La définition de ce diagramme, sous forme de clause en languge de programmation logique, est donnée ci-dessous. La clause est constituée de 3 arguments, représentant dans l'ordre la séquence des ESS, l’ensemble des liaisons hydrogènes et l’ensemble des chiralités, tous représentés sous forme de listes. Chaque SSE est defini dans le corps de la clause en triplet (N,T,D) où N représente le nombre associé a l'élément SSE de la séquence, T le type (b ou h) et D la direction (1 ou 0).
'2bopA0'([S1,S2,S3,S4,S5,S6,S7,S8],
[(S1,a,S6),(S1,a,S8),(S4,a,S6),(S5,a,S6)],
[(S1,r,S4),(S6,r,S8)] ):-
S1=(1,b,1), S2=(2,b,0), S3=(3,h,0), S4=(4,b,1),
S5=(5,b,1), S6=(6,b,0), S7=(7,h,1), S8=(8,b,0).
Un motif TOPS est comparable a un diagramme TOPS. C'est une généralisation de plusieurs diagrammes , se conformant aux caractéristiques topologiques communes de ceux-ci. Cette généralisation est obtenue grâce à l’insertion d'ESS (ainsi que leurs liaisons hydrogènes et chiralités) dans la séquence des éléments de structure secondaire. En somme, un diagramme est tout simplement un motif où aucune insertion n’est permise. La longueur d'une insertion doit être contenue dans la plage des longueurs de séquences autorisées pouvant être insérées. Un motif TOPS forme ainsi un triplet, similaire à celui du diagramme TOPS. Cette séquence d'ESS où les insertions sont permises est notée motif-T.
De façon formelle, un motif TOPS est un triplet P = (T,H,C) où T (dénoté motif-T) est une séquence V1 ¾ I1→ V2 ¾ I2→ … ¾ Ik-1→ Vk comprenant les ESS symbolisés par Vi et entre chacun de ces éléments, une description d’insertion. Chaque description d’insertion Ij représente une contrainte sur le nombre d'ESS pouvant être insérés à cette position. La plage potentielle de Ij varie, allant de zéro au nombre maximum d'ESS contenus dans un diagramme TOPS (environ 60). Nous utiliserons N ci-dessous pour représenter ce nombre maximum, et comme pour les diagrammes, H et C pour représenter respectivement une liaison hydrogène et une chiralité.
Prenons l’exemple d’un motif TOPS décrivant la tresse (la protéine 2bop est un exemplaire de tresse), illustré dans la figure 4.
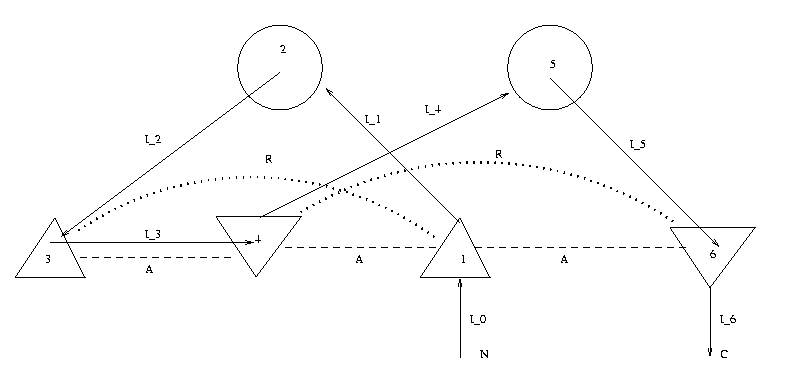
Figure 4. Diagramme TOPS du motif de tresse
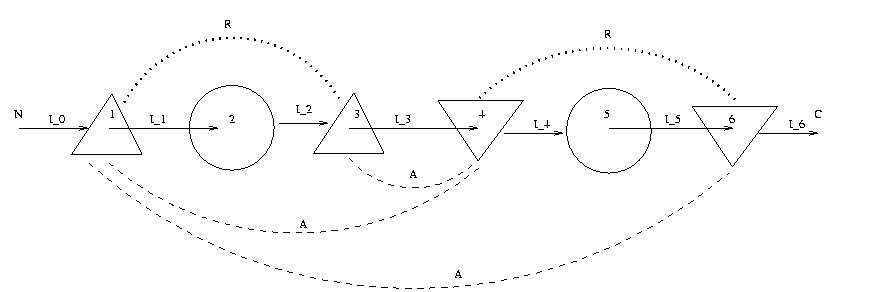
Figure 5. Diagramme linéaire TOPS du motif de tresse
En principe, comme dans les diagrammes TOPS, à chaque élément SSE d’un motif TOPS est associée une direction pointant vers le bas ou vert le haut (respectivement + ou -), et chaque élément est composé d’une lettre de l’alphabet {α, β}. Cependant, ιtant donné qu’un diagramme TOPS présente une invariance rotationnelle de 180o autour des axes x et y, il est nécessaire d’associer à chaque SSE du motif, une variable de direction, ⊕ ou ⊖ , de façon à satisfaire la contrainte suivante :
" ⊕, ⊖ є P : opp (⊕, ⊖)↔ (⊕ = +∧⊖ = -) V (⊕ = -∧⊖ = +)
La clause du motif de tresse ci-dessous a été écrite dans un langage de programmation logique par contrainte. Cette clause ressemble beaucoup en forme à celle du diagramme. Toutefois les nombres des ESS ne sont plus ici des exemples. Ces nombres sont contraints à être en ordre, les intervalles vides étant permis. Pour rester général, nous avons explicitement précisé chaque contrainte, plutôt que de les coder de façon récursive (dans certain motif, chaque intervalle vide peut être de différente taille). Nous définissons également opposite/2, contraignant chacun de ses arguments d’être +1 ou 0, et de ne pas être égal.
plait( [S1,S2,S3,S4,S5,S6],
[(S1,a,S4),(S1,a,S6),(S3,a,S4)],
[(S1,r,S3),(S4,r,S6)] ):-
S1=(N1,e,Haut), S2=(N2,h,Bas), S3=(N3,e,Haut),
S4=(N4,e,Bas), S5=(N5,h,Haut), S6=(N6,e,Bas),
N1 #> 0, N2 #> N1, N3 #> N2, N4 #> N3, N5 #> N4,
N6 #> N5, 60 #>= N6,
opposite(Bas,Haut).
opposite(X,Y) :- X in 0..1, Y in 0..1, X #\= Y.
Cet algorithme par retour-arrière (backtracking) filtre un motif TOPS dans un diagramme TOPS et retourne l'ensemble des pairs de sommets correspondants entre le motif et le diagramme ainsi que l'ensemble des dimensions des insertions correspondantes du filtrage. Notre algorithme de filtrage par retour-arrière peut retourner plusieurs résultats à partir d'un seul motif (voir ci-dessous). Ce filtrage, tel qu'il est défini par l'algorithme, est de forme faible, c'est un isomorphisme de sous-graphe non-inductif. L'article [GWNT99] contient une version d'un algorithme permettant un filtrage fort (isomorphisme de sous-graphe inductif).
Les contraintes utilisées dans cet algorithme permettent l'élagage de l'espace de recherche. Nous assumons ici l'existence d'un outil de résolution de contraintes pour équations et inéquations sur l'ensemble des nombres entiers. Avant tout, l'algorithme de filtrage impose initialement des contraintes sur les nombres des ESS du diagramme qui peuvent s'apparier aux nombres des ESS du motif. L'algorithme impose également des contraintes sur le nombre d'insertions entre les nombres des ESS qui s'apparient dans le diagramme. Ceci est réalisé lors de la phase 'Initialiser' en établissant (i) une correspondance entre chaque nombre des sommets du motif et la plage de nombres possibles des sommets du diagramme auxquels il peux s'apparier et (ii) une liste de la dimension des insertions correspondantes. Une fois que les valeurs des nombres des sommets s'appariant et des insertions sont établies, ces valeurs sont à nouveau contraintes d'abord à un filtrage sur les liaisons hydrogènes (filtrage-H) et ensuite sur les chiralités (filtrage-C). Pour terminer, le filtrage sur une séquence (filtraget-S) génère les nombres des ESS s'appariant dans le diagramme, ainsi que les valeurs des insertions correspondantes.
L'algorithme est le suivant:
Sachant que:
- le motif P = (T, Hp, Cp) et la contrainte correspondante opp(définie ci-dessus) sur l'ensemble des variables de direction (
- le diagramme Diag = (S,Hd,Cd)
Initialiser :
- Corr, la correspondance entre les nombres des sommets du diagramme et les nombres des sommets du motif, tel que Corr := (d1,d2,…,dk), où di (
Ins := (I0, I1, I2,…,Ik) où Ii (
C1 0 < di ≤ N, C2 di + Ii + 1 = di+1
Noter que la contrainte C1 définie la plage de di; C2 assure la préservation de la séquence ainsi que la prise en compte des contraintes sur la dimension des intervalles définies par Ii; N représente la taille de l'insertion la plus longue possible, en pratique moins de 60.
A effectuer dans l'ordre:
―
Filtrage-H: Hp ⊆ Hd, soit pour tout H-bond (Vi, δ, Vj) de Hp, trouver (Uk, δ, Ul) de Hd tel que:- La lettre Vi s'apparie a Uk, la lettre Vj s'apparie a Ul, et
- di = k et dj = l pour tout di, dj de Corr, respectant les contraintes C1, C2 et C3 sur k et l.
―
Filtrage-C: Cp ⊆ Cd, soit pour toute chiralité (Vi, χ, Vj) de Cp, trouver (Uk, χ, Ul) de cd tel que:- La lettre Vi s'apparie à Uk, et le caractère Vj s'apparie à Ul, et
- di = k et dj = l pour tout di, dj de Corr, respectant les contraintes C1, C2 et C3 sur k et l.
―
Filtrage-S: T s'apparie à S avec les intervalles: pour tout Vi de T, trouver Uk de S tel que dk = I soit dans Corr.Résultat: en cas de succès, toutes les pairs possibles (Corr, Ins), où Corr est l'ensemble des sommets correspondants, et Ins est l'ensemble des tailles d'insertions correspondantes pour cette comparaison.
Exemple de filtrages:
Pour filter le motif de tresse, motif ayant 6 SSE, dans le domaine 2bopA0, nous initialisons la correspondance Corr:= (d1,d2, d3, d4, d5, d6,), et les insertions Ins := (I0, I1, I2, I3, I4, I5, I6,), et imposons les contraintes C1 0 < di ≤ N, C2 di + Ii + 1 = di+1 comme indiqué ci-dessus.
―
Filtrage-H donne le résultat suivant: Corr := (1, d2, d3, 6,7,8) où d2 є 2…3, d3 є 4…5 etIns := (0, I1, I2, I3, ,0,0,0) où I1
,є 0…1, I2є 0…1, I3є 0…1 et I1+ I2+ I3=2―
Ensuite, Filtrage-C contraint davantage la correspondance et les valeurs des insertions:Corr := (1,d2,4, 6,7,8) où d2
є 2…3, et Ins := (0, I1, I2, 1 ,0,0,0) où I1,є 0…1, I2є 0…1 et I1+ I2=1―
Pour terminer, Filtrage-S donne les solutions alternatives suivantes:- Corr := (1,2, 4, 6,7,8) et Ins := (0,0,1,1 ,0,0,0)
- Corr := (1,3,4, 6,7,8) et Ins := (0,1,0,1 ,0,0,0)
(Voir figure 6: illustration de filtrages alternatifs).
Complexité de l'algorithme de filtrage d'un motif:
Supposons une séquence avec x liaisons hydrogènes et un motif avec s liaisons hydrogènes. Alors l'algorithme filtre tous les motifs de liaisons hydrogènes en temps H=Csx_= O((x! / s!) · (x-s)!
Dans le pire des cas, quand s=x/2 nous avons H=O(2x / Ö x).
De façon similaire, pour une séquence avec y chiralités, tous les motifs de chiralités sont filtrés en temps C=O(2y / Ö y).
Le temps total pour trouver tous les motifs de liaisons hydrogènes et chiralités n'excédera pas
T = C ·
H £
O(2n / Ö
n ) where n=x+y
Ceci dit, le temp d'exécution sur des exemples réels est considérablement plus faible: le pire des cas ne se produisant pas dans de vraies données biologiques.
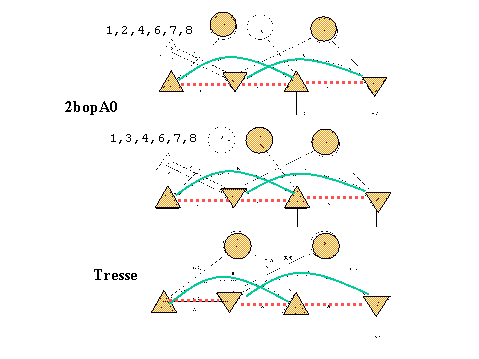
Figure 6. Domaine 2bop: filtrage d'une tresse
3.2 Implémentation en programmation logique par contraintes
Une implémentation simple de la version de cet algorithme de comparaison en programmation logique par contraintes est définie ci-dessous, avec un exemple d'appel utilisant les définitions du motif de tresse et la description du domaine 2bopA0 définis respectivement dans la section 2.1 et section 2.2.
?- plait (P_Seq,P_Hbonds,P_Chirs), '2bopA0'(D_Seq,D_Hbonds,D_Chirs),
match((P_Seq,P_Hbonds,P_Chirs), (D_Seq,D_Hbonds,D_Chirs)).
match((P_Seq,P_Hbonds,P_Chirs), (D_Seq,D_Hbonds,D_Chirs)):-
subseteq(P_Hbonds,D_Hbonds),
subseteq(P_Chirs,D_Chirs),
subseqeq(P_Seq,D_Seq).
où sont définis le sous ensemble (subseteq/2) et le filtrage de séquences avec intervalles (subseqeq/2):
subseteq([],Set2).
subseteq([X|Set1],Set2):-
member(X,Set2,Set2a),
subseteq(Set1,Set2a).
member(X,[X|Ys],Ys).
member(X,[Y|Ys],[Y|Zs]):- member(X,Ys,Zs).
subseqeq([],Seq2).
subseqeq([X|Seq1],[X|Seq2]):-
subseqeq(Seq1,Seq2).
subseqeq([X|Seq1],[_|Seq2]):-
subseqeq([X|Seq1],Seq2).
L'élagage par contraintes de liaisons hydrogènes et de chiralités est plutôt efficace, et la question est de savoir dans quel ordre commencer. Une contrainte de liaison hydrogène force un élément SSE d'être sous forme de brin et d'avoir une direction relative. Ceci permet un élagage beaucoup plus rapide de l'espace de recherche, plutôt que d'essayer de filtrer un motif-T sur une séquence. Il faut dire que les motifs-T sont nettement plus courts que les séquences des diagrammes et que les insertions permettent à un motif-T d'être apparié de bien des façons. Si tous les ESS du motif appartiennent à l'ensemble des liaisons hydrogènes, alors le filtrage est considérablement élagué.
Nous avons comparé le temps d'exécution de notre algorithme par contraintes avec le temps d'exécution d'une version par retour-arrière (génère et teste), version obtenue en remplaçant #=/2 par is/2 et en arrangeant l'ordre des appels dans l'algorithme de filtrage. Tous les arguments de droite de is/2 sont ainsi sans variables lorsque le prédicat est appelé. Cela veut dire essentiellement que les contraintes C1 et C2 sont contrôlées après avoir généré toutes les alternatives du filtrage. L'implémentation des deux versions a été réalisée en clp(FD) et exécutée sur un DEC Alpha. Les résultats sont présentés dans le tableau ci-dessous. On observe que le temps d'exécution de l'algorithme de filtrage augmente considérablement lorsque la version par retour-arrière est utilisée, allant de 1.4 pour 1à 68 pour 1. Ces résultats dépendent du nombre de brins et de feuillets dans le motif, ainsi que le motif des liaisons hydrogènes. Par exemple, sur une base de 3567 domaines, une requête pour un jelly roll de type 1 (8 brins et deux feuillets anti-parallèles avec un total de 6 liaisons hydrogènes) trouve ce motif 203 fois (dans 110 domaines: il existe plusieurs alternatives dans un même domaine). Le temps d'exécution est de 383351 ms pour la version par retour-arrière, comparé à 10719 ms pour la version par contraintes, soit 35 fois plus long.
|
Nom du motif |
Motif liaison hydrogène |
brins |
feuillet |
Liaison hydrogène |
Rapport temps Retour-arrière / contraintes |
Nbre de filtrages dans Atlas |
|
tresse |
4-1-3-2 |
4 |
1 |
3 |
1.4 |
47 |
|
Clé grecque 5 |
1-4-3-2-5 |
5 |
1 |
4 |
2.3 |
22 |
|
Pli Rossman |
3-2-1-4-5-6 |
6 |
1 |
5 |
1.8 |
46 |
|
IG |
2-5-6, 1-4-3 |
6 |
2 |
4 |
11 |
738 |
|
Jelly Roll 1 |
1-8-3-6, 2-7-4-5 |
8 |
2 |
6 |
36 |
203 |
|
Jelly Roll 2 |
8-1-6-3, 7-2-5-4 |
8 |
2 |
6 |
36 |
8 |
|
IG (V) |
1-2-7-6, 9-8-3-4-5 |
9 |
2 |
7 |
68 |
304 |
4 Motifs courants
Une bibliothèque de motifs bien connus a été conçue, comprenant des descriptions de haut niveau extraites de la littérature (voir [BT91]), incluant: les tresses, les motifs grecques, les jelly rolls, les domaines à NAD de Rossmann, les immunoglobulines, les tonneaux (b , TIM, et a /b ), les feuilles de trèfle et les hélices de bateau b .
5 Base de données
Nous avons converti et transféré tout le contenu de la base de données PDB (au février 2000) dans une base de diagrammes TOPS sous format de programmation logique. Ceci a été réalisé en 3 opérations: une première analyse est effectuée par le programme DSSP [KS83], programme localisant les ESS et les liaisons hydrogènes atomiques. Cette information est ensuite utilisée par le programme TOPS [FMT94, WSFT99] qui en fait une analyse topologique ainsi qu' une analyse par domaine. Le nombre de domaines augrmente en moyenne de 500 par connection de chiralités. Le fichier résultant de cette analyse est alors traduit en diagramme TOPS sous format de programmation logique, ceci grâce à un compileur que nous avons développé en programmation logique par contraintes sur domaines finis. De plus, un ensemble représentatif de domaines de protéines ( "Atlas" TOPS) a été construit [WHT98], basé sur les structures de regroupement de la banque de données structurales, à 95% de similarité de séquences, et contient à ce jour plus de 3000 membres. Nous avons également converti en graphe TOPS l’ensemble SCOP PDB90 [MBHC9], domaines représentatifs, et l’ensemble CATH [OMJ+97], domaines non-identiques representatifs N-Reps, contenant chacun un peu plus de 3000 domaines.
Nous reconnaissons qu’à long terme il sera de plus en plus difficile de stocker les definitions TOPS de domaines sous fichiers Prolog et qu’un système de gestion de base de données beaucoup plus sophistiqué, tel un système industriel, deviendra nécessaire. Notre collection contient 24569 domaines, provenant de la base PDB, soit un total de 37.7 MB. Cela représente une moyenne de 1.5KB par domaine. Le taux de stockage dans la base PDB est d’environ 150 structures par mois. Avec 2 à 3 domaines par protéine, cela nous donne une moyenne de 500 domaines par mois. Outre ce problème, les données de structures de la base PDB sont régulièrement mises à jour ou supprimées, chose difficile à réaliser dans notre système de fichiers – les mises à jour sont effectuées en re-convertissant tout le contenu de la base PDB. Ce processus est très long (environ 4 heures ½ sur un DEC Alpha), s'expliquant par l'exécution des programmes DSSP [KS83] et TOPS [WSFT99]. Ce taux de stockage ne va probablement pas diminuer. Bien au contraire, les recherches effectuées sur le génome humain et autres organismes génèrent des quantités énormes de séquences de protéines dont les structures n'ont pas encore été identifiées.
Nous étudions actuellement la possibilité d'utiliser un modèle relationnel de base de donnée, connecté a notre système de recherche de motifs, ceci afin de prévenir des problèmes de stockage (quantité énorme de données générée régulièrement) et de leurs mises à jours. Une base de données Oracle (version 7.3) contenant les diagrammes TOPS a été développée. Ces diagrammes proviennent de notre base de données en programmation logique, et sont traduits grâce à un script Prolog. Des tests initiaux montrent que des requêtes simples peuvent etre construites en SQL, équivalentes à celles de notre système de programmation logique par contraintes, par exemple la recherche des tournures gauchères
αβα (left-handed αβα turn). Sur les 3567 domaines de l'Atlas, nous avons identifiι 151 tournures gauchères αβα, soit 4.23%. La base de donnιes N-Rep CATH en contient 3.28% et la base SCOP PDB90 en contient 5.54%. Ces types de domaines sont importants en biologie car ils sont thermodynamiquement instables.La prochaine étape de notre étude est maintenant de savoir si notre mécanisme de filtrage de motifs peut être implementé de facon efficace en Oracle, ou si une interface de connexion entre notre système de programmation logique par contraintes et le système de gestion de base de données Oracle devra être développée.
6 Details de l'implémentation
Le programme de filtrage de motifs, tout comme les programmes de comparaison de structures et de découverte de motifs qui ne sont pas décrits dans ce document, ont été développés sous programmation logique par contraintes sur domaines finis. Ces programmes s'exécutent sous gprolog (
http://pauillac.inria.fr/diaz/gnu-prolog) et également sous SICStus Prolog, faisant usage de la bibliothèque clpfd (http://www.sics.se/sicstus.html). Le système de production s'execute sur le serveur web DEC Alpah de l'Institut Européen de Bio-informatique, utilisant un code executable produit par clp(FD), ceci étant du à l'absence de port gprolog sur cette plateforme pour le moment. La version de l'Atlas TOPS en programmation logique contient plus de 3000 définitions de domaines. Rappelons que la base PDB contient plus de 24 000 définitions. Le temps de chargement est d'environ 3 secondes par mega-octet, soit approximativement 75 secondes pour le chargement complet de toute la base de donnée PDB. L'atlas peut être chargé en mémoire sur le serveur, cependant un mécanisme simple de paging pour base de données a été développé dans le but de surmonter les restrictions mémoire lorsque des requêtes interrogant tout le contenu de la base de données PDB sont composées. L'interface web du programme de recherche de motifs a été crée avec une version de PiLLoW, que nous avons branché au clp(FD).7 Site Web
Le système est disponible sur le site web TOPS de l'Institut Européen de Bio-informatique: tops.ebi.ac.uk/tops/topsQ.html. Ce site est également un site d'accueil d'autres services tels que:
- outil d'exploration de l'Atlas de croquis, sélection par nom de domaines de protéines, recherche par motif topologique (le résultat de la recherche offre la possibilité de visualiser les croquis TOPS)
-outil de génération de croquis TOPS à partir de fichier TOPS soumis par l'utilisateur
- outil de comparaison rapide entre descriptions de protéines et la base PDB ou une variété d'un sous-ensemble représentatif.
Le logiciel de génération, d'édition et de visualisation des croquis est téléchargeable à partir de ce site, on y trouve également des articles en-ligne sur le sujet.
8 Conclusion
La représentation des structures de protéines au niveau abstrait de la topologie nous a permis de développer une méthode de filtrage rapide de motifs sur une base de données topologiques de protéines. Cette rapidité est obtenue grâce aux contraintes qui permettent un élagage de l'espace de recherche de l'algorithme de filtrage de motifs. Le language clp(FD) fut choisit dans l'implementation du système pour ses qualités d'exécution rapide des programmes et la disponibilité du système.
Cette technique de flitrage forme également la base d'un algorithme de découverte de motifs qui utilise l'extension repétée de motifs ainsi que le filtrage de motifs [GWVT00]. Nous sommes actuellement en train d'étudier l'introduction de coefficients de filtrage afin de mieux diriger le processus de découverte des motifs.
Nos travaux sur la découverte de motifs [GWVT00] se rapportent à ceux de Turcotte et al [TMS98] qui utilisent la programmation logique inductive (PLI) afin de découvrir les règles gouvernant la topologie à tri-dimensionnelle des structures de protéines. Il y a cependant des différences. Tout d'abord, Turcotte et al utilisent un système PLI spécialisé (Progol) sans computation de contraintes et invoquent des règles beaucoup plus générales, autres que les motifs structuraux. Leur système, par exemple, exploite les informations contenues au niveau de la chaîne primaire (les acides aminés). Ce systéme est aussi nettement plus lent (Turcotte, personal communication). Dans les travaux de Turcotte et Al, les règles produites incorporent un nombre d'éléments de structures secondaires, typiquement 2 à 4 alors que notre approche vise à maximiser le nombre d'éléments inclus dans un motif. Leur fitrage et méthodologie est un filtrage simple de prédicats alors que l' algorithme que nous venons de décrire dans cet article est hautement spécialisé.
Remerciements
Les auteurs désirent remercier Alvis Brazma de l'EBI pour ses suggestions inestimables, et Juris Viksna pour son aide sur les mesures de complexité.
Annexe I
Ce document est une version mise à jour de l'article 'A declarative technique for constraint-based protein topology pattern matching', publié à l'origine en anglais.
Bibliographie:
[ABB+87] E.E. Abola, F.C. Bernstein, S.H. Bryant, T.F. Koetzle, and J. Weng. Protein Data Bank. In F. H. Allen, G. Bergerhoff, and R. Sievers, editors, Crystallographic Databases-Information Content, Software Systems, Scientific Applications, pages 107-132. Data Commission of the International Union of Crystallography, Bonn/Cambridge/Chester, 1987.
[BKW+77] F.C. Bernstein, T.F. Koetzle, G.J.B. Williams, E.F. Meyer, Jr., M.D. Brice, F. R. Rodgers, O. Kennard, T. Shimanouchi, and M. Tasumi. The Protein Data Bank: a Computer-based Archival File for Macromolecular Structures. Journal of Molecular Biology, 112:535-542, 1977.
[BT91] C. Brandon and J. Tooze. Introduction to protein structures. Garland Publishing, 1991.
[FMT94] T.P. Flores, D.M. Moss, and J.M. Thornton. An algorithm for automatically generating protein topology cartoons. Protein Engineering, 7(1):31-37, 1994
[GMB96] J-F. Gibrat, T. Madej, and S. H. Bryant. Surprising similarities in structure comparison. Curr. Opin. Struct. Biol., 6:377-385, 1996
[GWNT99] D. R. Gilbert, D. R. Westhead, N. Nagano, and J. M. Thornton. Motif-based searching in tops protein topology databases. Bioinformatics, 15(4):317-326, 1999.
[GWVT00] David Gilbert, David Westhead, Juris Viksna, and Janet Thornton. Topology-based protein structure comparison using a pattern discorvery technique. In Proceedings of AISB-00 Symposium on AI in Bioinformatics. ISBN 1 902956 12 X, pp 11-17, Society for the Study of Artificial Intelligence and the Simulation of Behaviour, 2000.
[HGLS92] R. S. Hegde, S. R. Grossman, L. A. Laimins, and P. B. Sigler. Crystal structure at 1.7 A of the bovine papillomavirus-1 E2 DNA-binding domain bound to its DNA target. Nature, 359(6395):505-512, Oct 1992.
[KS83] W. Kabsch and C. Sander. Dictionary of protein secondary structure: Pattern recognition of hydrogen-bonded and geometrical features. Biopolymers, 22:2577-2637, 1983.
[MBHC95] A. G. Murzin, S.E. Brenner, T. Hubbard, and C. Chotia. Scop: a structural classification of proteins database for the inverstigation of sequences and structures. Journal of Molecular Biology, 247-536-540, 1995.
[OMJ+97] C. A. Orengo, A. D. Michie, D. T. Jones, M. B. Swindells, and J. M. Thornton. CATH - a hirearchic classification of protein domain structures. Structure, 5(8):1093-1108, 1997.
[Ore94] C. Orengo. Classification of protein folds. Current Opinion in Structural Biology, 4:429-440, 1994.
[SMW95] R. A. Sayle and E. J. Milner-White. RASMOL: biomolecular graphics for all. Trends in Biochemical Sciences, 20(9):374, Sep 1995.
[ST77] M.J.E. Sternberg and J. M. Thornton. On the conformation of proteins: The handedness of the connectoon between parallel beta strands. Journal of Molecular Biology, 110:269-283, 1977.
[TMS98] M. Turcotte, S. H. Muggleton and M. J. E. Sternberg, Application of Inductive Logic Programming to Discover Rules Governing the Three-Dimensional Topology of Protein Structure, Proceedings of the 8th International Conference on Inductive Logic Programming, LNAI 1446:53-64, 1998.
[WHT98] D. R. Westhead, D. C. Hutton, and J. M. Thornton. An atlas of protein topology catoons available on the World Wide Web. Trends in Biochemical Sciences, 23, 1998.
[WSFT99] D. R. Westhead, T. W. F. Slidel, T. P. J. Flores, and J. M. Thornton. Protein structural topology: automated analysis and diagrammatic representation. Protein Science, 8(4):897-904, 1999.