The overall objective of the research work is to study the foundational
aspects of the problem of program verification with the purpose of
constructing a theory of
verification which serves as a rigorous basis for the design of an
automatic program verifier.
The practical outcome of this preliminary formal activity should be the
realization of a prototype verifier for logic programs, whose relevance
for solving ``real-life'' problems should be tested on a wide range of
examples.
The automation of reasoning about computer programs is one of the main
objectives in the field of program verification.
To this aim, mechanical theorem-proving is crucial.
As a result, formal proofs seem to be attractive, and, indeed,
there are now a number of techniques for obtaining in a formal system an
expression whose formal proof or disproof constitutes a verification that
a given program has a given property.
The tendency is, roughly, to represent properties of programs as theorems
in the first-order predicate calculus; in this form established mechanical
theorem proving techniques might be relevant to automating the
verification process.
By restricting the attention on logic programs, we dispose of a very
specialized theorem-prover which is SLD-resolution. The idea is, then,
to use resolution-based techniques (e.g. some extensions of the
SLD-resolution) for proving properties of logic programs.
The main problem in doing so is that the resolution theorem-proving
tradition does not handle axiom schemes, such as mathematical induction.
And, as argued by almost all authors in the field, induction in one form
or another is unavoidable in proving properties of programs.
This is because the objects about which computer programmers think
(integers, sequences, trees, lists etc.) are usually inductively defined
concepts.
Moreover, a program can be seen as a finite description of a usually
infinite class of arbitrarily long computation sequences: induction is
a finite process by which the infinite can be defined.
Therefore, it seems necessary to find out a way to incorporate the power
of induction in a resolution-based framework and use query
evaluation for the proofs of logic program properties.
There are two possibilities: one of them tries to get the effect of
induction by means of some loop detection tools; the other one faces
the problem directly by using a higher order logic
language in which simply typed 
-terms can express
the inductive nature of a specification formula.
The first approach is based on the view of program properties as integrity constraints, and has been previously investigated by Kowalski ([22]) and Lever ([23]). In Logic Programming, integrity constraints are often written as queries that can be evaluated by SLDNF-resolution, [8,24] (or some variants of it). One of the problems with this approach is that, as most properties of interest involve recursively defined predicates, evaluation of properties expressed as queries commonly generates infinite trees. Since the existence of an infinite failed SLDNF-resolution for a property is not in itself sufficient to determine that the property is a consequence of the completion of the program, soundness results are not easy to achieve. In [23] the use of SLS-resolution instead of SLDNF-resolution eliminates these difficulties. Another problem with the use of SLDNF-resolution is that negation by failure doesn't correctly treat variables. We propose to avoid this problem by using an extension of the Negation As Failure rule, which is able to deal with existentially quantified negative queries, namely the Negation As Instantiation rule (NAI, [15]). By augmenting NAI by loop detection we could avoid the problem with the infinite branches, which still remains in the interpreter extended by the NAI rule. Since the interpreter of LP palys a fundamental role in this approach, we believe that this can be generalized to other logic programming languages, such as constraint logic programming [20], and concurrent constraint programming [27,28], by considering the interpreters for those languages instead of Prolog.
As for the second approach, the starting point of the research is the observation that induction axiom schemata are in effect really just single second-order formulas
with the second-order quantifier dropped:
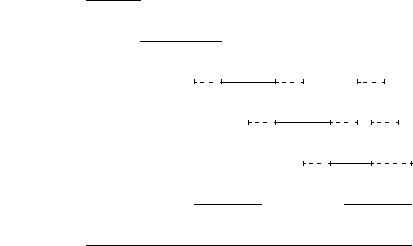
so that one can substitute any predicate 
, where S
is any first order sentence with one free variable k,
for P and get an axiom.
Thus, a higher-order logic programming
language like 
-Prolog ([26,25]) could be used to
implement such theorem
proving systems.
However, building a prover could be very complicated.
An alternative could be to use already existing systems, such as
the Isabelle theorem prover ([17,18]), which is built on higher-order
resolution, augmented with theories for doing induction.
The Coq system could also be a good candidate, since
it has higher-order quantification and induction even though it has not
resolution.