Bioinformatics - Lab 10
Model checking in systems biology
Robin Donaldson

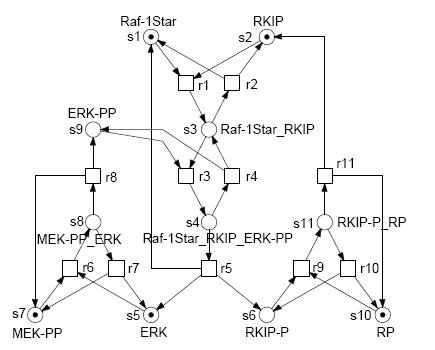
In this lab you will perform model checking of an example biochemical systems. This will be done against both the familiar deterministic simulation (BioNessie) and unfamiliar stochastic simulation (Gillespie algorithm).

This lab refers to the slides from the lecture on Model checking.

Software

MC2:

• Checks simulations for desired behaviour; both deterministic and stochastic simulations.
• Fast and parallelisable.
• Can instantiate variables within the behaviour.
• You will be given the location for the program and related files in the lab.

Biochemical Pathway

Exercise 1

This exercise requires you to perform deterministic model checking -- checking the single, average behaviour of the pathway. As such, you can ask questions about the pathway's behaviour in the average case, returning a true/false answer (probability 1/0). The RKIP model has been simulated in BioNessie using ODEs for a time for 100 seconds. This output is included in the file, rkip.bionessie.input. Take a look at this file using the command less rkip.bionessie.input and confirm that this is a simulation from BioNessie.

The query file rkip.bionessie.queries contains example properties. To perform model checking of these properties, run the following command:

java -jar MC2.jar det rkip.bionessie.input rkip.bionessie.queries

What do each of these properties mean?

Questions:

Add new queries to the rkip.bionessie.queries file to answer the following questions. Each query should be on a new line, and the questions below may need more than one query each.

1. Which of the following is true?
        - concentration of MEKPP is always higher than ERKPP
        - concentration of ERKPP is always higher than MEKPP

2. For which concentration range below is the protein MEKPP stable in after 50 seconds?
        - 500-600
        - 600-700
        - 700-800

   hint: this was done in class - use three queries.

3. Does the Raf1StarRKIP complex peak?
        - if so, at what time?

   hint: this was done in class. to find the time, use a variable.

4. At what time does protein RP reach its maximum concentration?

   hint: use the finally (F) operator with the max function and use a variable.

Exercise 2

This exercise requires you to perform stochastic model checking -- checking a range of behaviours of the pathway. As such, you can ask questions about how often a pathway exhibits the behaviour, returning a probability value in the range 0-1. A probability of 0.3 can be read as, "there is a 30% chance of the pathway exhibits the behaviour". The RKIP model has been simulated using Gillespie simulation for a time for 100 seconds. This output is included in the file, rkip.gillespie.input. Take a look at this file using the commandless rkip.gillespie.input and confirm that this is 100 simulations which are all different (noisy).

The query file rkip.gillespie.queries contains example properties. To perform model checking of these properties, run the following command:

java -jar MC2.jar stoch rkip.gillespie.input rkip.gillespie.queries --numtraces=1

The --numtraces=1 flag restricts memory to holding 1 simulation output at any time, to avoid overflowing the heap. Notice that you now get a probability value in the range 0-1, not simply a true/false (1/0).

Questions:

Add new queries to the rkip.gillespie.queries file to answer the following questions. Each query should be on a new line, and the questions below may need more than one query each.

1. What is the probability of each of the following?
        - concentration of MEKPP is always higher than ERKPP
        - concentration of ERKPP is always higher than MEKPP

2. What is the probability that the protein MEKPP is stable after 50 seconds in each concentration range below?
        - 500-600
        - 600-700
        - 700-800

   hint: this was done in class - use three queries.

3. At what times does protein RP reach its maximum concentration?

   hint: use the finally (F) operator with the max function and use a variable.